Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 5.Problemas - Ex. 57
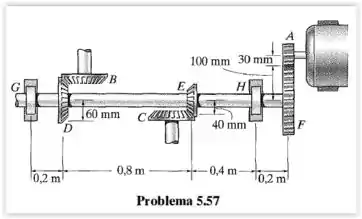
O motor produz um torque na engrenagem . Se a engrenagem travar repentinamente e parar de girar, mas puder girar livremente, determine o ângulo de torção de em relação a e de em relação a do eixo de aço L2 cujo diâmetro interno é e diâmetro externo é . Calcule também a tensão de cisalhamento máxima absoluta no eixo. O eixo está apoiado em mancais em e .
Passo 1
Olá, pessoal! Tudo bem com vocês?
O enunciado nos fornece os seguintes dados:
Aço L2, portanto,
Começaremos calculando o torque na engrenagem . Sabemos que:
Em que R é o raio da engrenagem. Então:
Como , temos que:
Passo 2
Vamos então calcular o ângulo da engrenagem em relação as engrenagens e .
Analisando a figura no enunciado, percebemos que os ângulos e será o mesmo, pois se a engrenagem parar, para de girar e, consequentemente, o movimento da também vai ser interrompido. Portanto:
O momento polar de inércia, , é dado por:
Simplificando e substituindo os valores, temos:
Passo 3
Vamos agora encontrar a tensão de cisalhamento máxima:
Que substituindo o momento polar de inercia e simplificando, fica:
E então colocando os todos as dados, temos: