Enunciado
Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 12.Problemas - Ex. 210
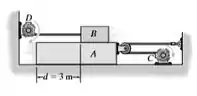
O motor em C puxa o cabo com uma aceleração de m/s2, onde t é dado em segundos. O motor em D puxa o cabo a . Se ambos motores partem ao mesmo tempo do repouso quando d=3m, determine (a) o tempo necessário para d=0, e (b) as velocidades dos blocos A e B quando isso ocorre.
Passo 1
Para o bloco A, temos que
Derivando a equação para encontrar a velocidade e a aceleração
A equação da velocidade e espaço percorrido do bloco A serão, respectivamente
Passo 2
Para o bloco B, temos que
A equação da velocidade e espaço percorrido do bloco A serão, respectivamente
Como
Então a equação será
Resolvendo a equação biquadrada, temos que
A velocidade pode ser calculada a partir da equação abaixo
E a velocidade em B será
Resposta
A velocidade em A e B serão, respectivamente 0,605 m/s e 5,33 m/s