Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 12.Problemas - Ex. 205

A extremidade da corda em B é puxada a uma velocidade vb=2m/s e esta velocidade diminui a uma taxa de 1m/s², em um dado instante. Determinar as velocidades e aceleração de em A.

Passo 1

Vamos analisar a imagem e fazer as considerações a respeito do comprimento L das cordas.

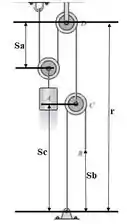
Podemos dividir o comprimento total L da corda em 2 novos comprimentos, L1 e L2, onde:

2 S a + r - S c = l 1

2 S a - S c = l 1 - r (1)

E,

2 S c - S b = l 2         (2)

Somando as equações (1) e (2), podemos rearranjar uma nova equação.

4 S a - S b = 2 l 1 - 2 r + l 2           (3)

Passo 2

Derivando a equação (3) obtida, temos que:

4 v a - v b = 0

E, derivando novamente para achar a aceleração:

4 a a - a b = 0

Logo teremos que:

v b = 4 v a

E,

a b = 4 a a

Passo 3

Subistituindo o valor de vb=2m/s e ab=-1m/s², na equação encontrada, temos:

v a = 2 4 = 0,5 m / s

E,

a a = ( - 1 ) 4 = - 0,25 m / s ²

Resposta

Quando a extremidade em B é puxada a uma velocidade de 2m/s que desacelera a uma taxa de 1m/s², o bloco em A se movimenta com uma velocidade escalar de 0,5m/s e desecelera a uma taxa de -0,25m/s².

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Para o instante representado, o carro A tem uma aceleração na direção do seu movimento, e o carro B tem uma velocidade de 72k m / h que está aumentando. Se a aceleração de B como observada a partir de
Para o instante representado, o carro A tem uma velocidade de 100k m / h , que está aumentando na taxa de 8k m / h cada segundo. Simultaneamente, o carro B também tem uma velocidade de 100k m / h enqu
O pequeno avião A inicialmente voando para o norte com uma velocidade em relação ao solo de 225k m / h encontra um vento oeste de 75k m / h (soprando para o leste). O avião B voando para o oeste com u
Uma mulher P caminha em uma rua de leste para oeste a uma velocidade de 6k m / h . O vento sopra do noroeste como mostrado a uma velocidade de 4k m / h . Determine a velocidade do vento em relação à m
O carrinho de mineração C é puxado pelo motor M através de um conjunto de cordas e polias. Determinar a velocidade do ponto P de tal maneira que a velocidade escalar de C seja v c = 2 m / s .