Enunciado
Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 11.Problemas - Ex. 90
O movimento de uma partícula e definido pelas equações x = 2 cos t e y = 1 4 cos 2 t, onde x e y são expressos em metros e t e expresso em segundos. Mostre que a trajetória da partícula e parte da parábola mostrada, e determine a velocidade e a aceleração quando (a) t = 0, (b) t = 1,5 s.
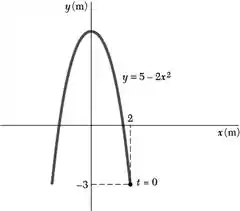
Passo 1
E ai gurizada tudo belezinha ? O enunciado pede que a gente encontre a velocidade e a aceleração quando (a) t = 0, (b) t = 1,5 s.
Nós temos
Então
Agora
e
Passo 2
- Em t = 0: vx = 0 vy = 0
- Em t = 1.53: vx = -2 sin (1.5) = 2 m/s
Passo 2
Resposta
Exercícios de Livros Relacionados
Para a partícula do Problema 11.63, trace a curva a-t e determine usando o método da Seção 11.8, (a) a posição da partícula quando t = 52 s, (b) o valor máximo de sua posição coordenada.
Três crianças estão jogando bolas de neve umas nas outras. A criança A joga uma bola de neve com velocidade horizontal v0. Se a bola de neve passa sobre a cabeça da criança B e atinge a criança C, det
O movimento amortecido de uma partícula que vibra e definido pelo vetor de posição r = x1(1 – 1/t(t + 1))i + (y1 e - π t / 2 cos 2 π t)j onde t e expresso em segundos. Para x1 = 30 mm e y1 = 20 mm, de
O movimento de uma partícula e definido pelas equações x = t2 - 8t + 7 e y = 0,5t2 - 2t - 4, onde x e y são expressos em metros e t em segundos. Determine (a) a intensidade da menor velocidade atingid