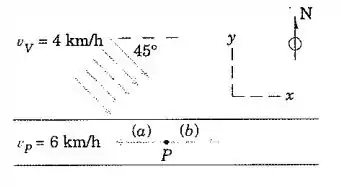
Uma mulher caminha em uma rua de leste para oeste a uma velocidade de . O vento sopra do noroeste como mostrado a uma velocidade de . Determine a velocidade do vento em relação à mulher se ela

(a) caminha para o oeste e

(b) caminha para o leste na rua.

Expresse seus resultados tanto em termos dos vetores unitários e como em módulos e direções da bússola.

Para descobrir o módulo , fazemos assim:

E o ângulo que a velocidade relativa faz com a direção oeste-leste (eixo ) satisfaz:

Isso significa que a velocidade relativa tem um módulo de apontando a abaixo do leste.

(b) O que muda aqui é a troca de sentido da velocidade da mulher, ou seja:

Como antes, a velocidade do vento será:

Então a velocidade relativa do vento em relação à mulher passa a ser:

Calculamos o módulo como antes:

E também o ângulo :

Isso significa que a velocidade relativa tem um módulo de apontando a abaixo do oeste.