Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 2.7 - Ex. 175
Um robô industrial está sendo utilizado para posicionar uma pequena peça . Calcule o módulo da aceleração de para o instante em que se graus por segundo e graus por segundo ao quadrado neste mesmo instante. A base do robô está girando na taxa constante graus por segundo. Durante o movimento os braços e permanecem perpendiculares.
Passo 1
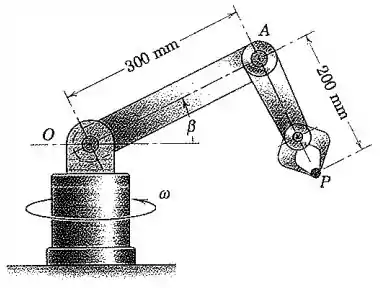
Galera, vamos tratar o problema usando coordenadas cilíndricas, de modo que a distância vai do chão até o ponto e a distância será considerada do ponto até a vertical do robô, conforme mostra a figura:
Então, considerando as dimensões e como mostradas na figura, podemos escrever assim:
Derivando essa equação em relação ao tempo, obtemos:
Derivamos novamente, utilizando a regra do produto:
Analogamente, olhamos para a figura e escrevemos , derivando como fizemos para :
Passo 2
Agora, vamos substituir os seguintes valores:
nas equações obtidas no passo anterior:
Para , só precisaremos da segunda derivada, como veremos adiante:
Por último, como a base do robô gira com velocidade (constante) perpendicular a , temos essa velocidade na direção de . Portanto,
Passo 3
Show! Agora temos todos os valores para substituir na expressão da aceleração em coordenadas cilíndricas:
Então as componentes são:
Enfim, podemos calcular o módulo da aceleração: