Enunciado
Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 12.Problemas - Ex. 209
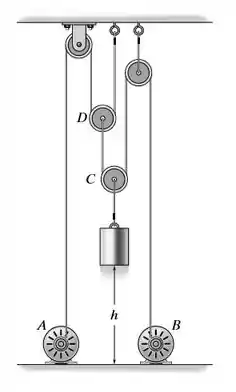
Se os motores em A e B recolhem seus cabos conectados com uma aceleração a=0,2t m/s2, onde t é dado em segundos, determine a velocidade escalar do bloco quando ele alcança uma altura de h=4m, partindo do repouso em h=0. Além disso, determine quanto tempo ele leva para alcançar esta altura.
Passo 1
Realizando uma análise nas cordas e polias temos que:
Então a variação será
Como
Resolvendo as equações, teremos que
Passo 2
A partir da equação , temos que
Resolvendo a integral, a velocidade será
De modo análogo, podemos encontrar o espaço percorrido a partir da equação , então
Então o espaço será
s
Passo 3
Como foi calculado o tempo, podemos calcular a velocidade a partir da equação
Então a velocidade será
m/s
Resposta
O tempo e a velocidade serão, respectivamente 5,43 s e 2,9474 m/s
Exercícios de Livros Relacionados
No sistema de polias abaixo, a extremidade A do cabo é puxada a 5m/s, determinar a velovidade escalar vb do cilindro B.
Determinar a velocidade escalar do elevador se cada motor recolher o cabo a uma velocidade constante de 5m/s.
Determinar a velocidade escalar que o bloco B sobe quando a extremidade do cabo em A é puxada para baixo com velocidade escalar va=2m/s.
Determinar a velocidade escalar do bloco B, quando o bloco A se desloca para baixo com velocidade escalar de 2m/s e o bloco C se desloca para cima com velocidade escalar de 1m/s.
Se o caminhão se desloca a uma velocidade de escalar constante vT = 1,8 m/s, determine a velocidade escalar da caixa para qualquer ângulo θ da corda. A corda tem um comprimento de 30 m e passa sobre u