Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 2.8 - Ex. 195
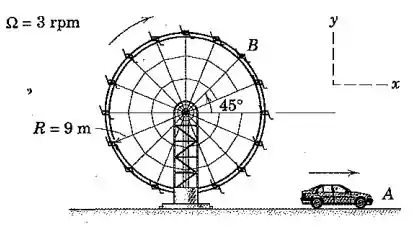
O carro tem uma velocidade para a frente de e está acelerando a . Determine a velocidade e a aceleração do carro em relação ao observador , que é levado em uma cadeira sem rotação sobre a roda-gigante. A velocidade angular da roda-gigante é constante.
Passo 1
Vetorialmente, podemos escrever a velocidade do carro e do observador desse modo:
Porém, o módulo da velocidade do observador é dado assim:
Então:
Assim, já podemos calcular a velocidade relativa do carro em relação ao observador :
Passo 2
A aceleração do carro pode ser escrita assim:
O módulo da aceleração do observador é dado pela fórmula da aceleração normal para movimento circular:
Vetorialmente, escrevemos assim:
Assim, já podemos calcular a aceleração relativa do carro em relação ao observador :