Enunciado
Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 4.Problemas de Revisão - Ex. 198
As quatro forças mostradas na figura abaixo são aplicadas a uma placa rígida suportada por um poste de aço cheio de raio . Sabendo que e , determine a tensão máxima no poste quando a força em é removida e quando as forças em e também são removidas..
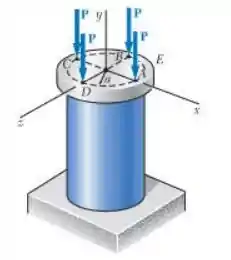
Passo 1
Fala aí, galera. Beleza? Bora resolver mais um exercício pra tirar aquele notão.
Sabemos que para uma seção circular de raio , a área da seção vai ser:
E o momento de inércia vai ser:
Assim, podemos determinar a tensão. Ela é dada por:
Como . E temos quatro forças de módulo , temos:
Passo 2
Para o primeiro caso, em que a força é removida, temos:
Com isso, a tensão máxima no poste vai ser:
Substituindo:
Passo 3
Para o segundo caso, em que as forças e são removidas, temos:
Assim, o momento resultante em módulo vai ser:
Logo, a tensão máxima no poste vai ser:
Substituindo:
É isso, galera!!! Bora zerar esse livro?