Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 5.Problemas - Ex. 229

Um objeto flutuante sólido é composto de um hemisfério e um cone de raio igual r feito do mesmo material homogêneo. Se o objeto flutuar com o centro do hemisfério acima da superfície da água, encontre a altitude máxima h que o cone pode ter antes que o objeto não flutue mais na posição vertical ilustrada.

Passo 1

Fala galera, tudo certo? Bora fazer mais um exercício? Prometo que vai ser bem rapidinho!

O enunciado nos pede para determinar a altitude máxima h do cone para que o objeto se mantenha na posição mostrada.

Então bora resolver! Para resolver este problema vamos começar fazendo o diagrama de corpo livre do objeto.

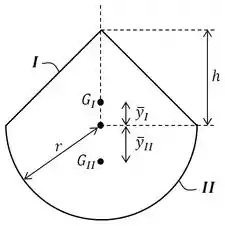
Passo 2

Esse exercício pode ser resolvido de uma forma bem simples! Para analisar o equilíbrio do corpo, vamos dividi-lo em dois objetos: o cone I e a meia esfera I I . Para que ele esteja em equilíbrio temos que satisfazer:

V I * y - I = V I I * y - I I

Com o auxílio da Tabela D/4 de propriedades de sólidos homogêneos do livro, temos que as coordenadas y - I do cone e y - I I da meia esfera são:

y - I = h - 3 h 4 = h 4

y - I I = 3 r 8

E os volumes do cone e da meia esfera:

V I = 1 3 π r 2 h

V I I = 1 2 * 4 3 π r 3 = 2 3 π r 3

Passo 3

Show de bola! Substituindo então esses valores na equação de equilíbrio:

V I * y - I = V I I * y - I I

1 3 π r 2 h * h 4 = 2 3 π r 3 * 3 r 8

π r 2 h 2 12 = π r 4 4

h 2 = π r 4 4 * 12 π r 2

h = 3 r 2

h = r 3

É só isso, galera. Dá pra acreditar?

Partiu pra próxima!

Resposta

h = r 3

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine a área da superfície interior do pistão de freio. Ele consiste em uma peça completamente circular. Sua seção transversal aparece na figura.
Determine o volume do material necessário para realizar a moldagem.
O trocador de calor irradia energia térmica a uma taxa de 2500k J / h para cada metro quadrado de sua área superficial. Determine quantos joules ( J ) são irradiados dentro de um período de 5 horas.
Determine a altura h à qual o líquido deve ser vertido dentro do copo cônico de modo que atinja três quartos da área de superfície no interior do copo. Para o cálculo, desconsidere a espessura do copo
A corrente da esquerda para a direita no fluxo causa um arrasto uniforme de 4 lb por pé do fluxo cruzado no cabo flutuante que é conectado aos postes A e B. Determine as tensões mínimas e máximas no c