Enunciado
Mecânica e Resistência dos Materiais - Hibbeler - Estática- Ed: 14º - Capítulo 9.Problemas - Ex. 107
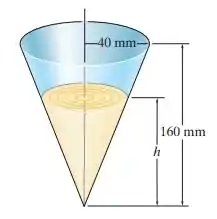
Determine a altura à qual o líquido deve ser vertido dentro do copo cônico de modo que atinja três quartos da área de superfície no interior do copo. Para o cálculo, desconsidere a espessura do copo.
Passo 1
Fala aí, galerinha do Responde aí. Tudo bem? Bora pra mais uma questão de Estática.
Neste problema, temos que determinar a altura de um líquido de modo que atinja três quartos da área de superfície no interior do copo. Então, vamos determinar a área total, ou seja, a superfície do recipiente.
Sabemos que a área de um cone é dada por:
Onde:
Podemos planificar o cone, assim, teremos o seguinte triângulo:
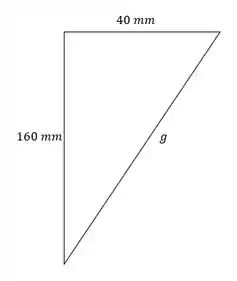
Com isso, vamos utilizar o teorema de Pitágoras para encontrarmos a geratriz, temos:
Agora que achamos a geratriz, podemos encontrar a superfície do copo. Basta substituir naquela fórmula que eu mostrei lá em cima. Bora lá:
Passo 2
Em seguida, como o enunciado nos informa, o líquido ocupa um volume que corresponde a parte inferior do copo até a uma altura , onde a área do copo até este ponto equivale a três quartos da da superfície total, ou seja:
Para encontrarmos o novo raio , vamos utilizar a semelhança de triângulos:
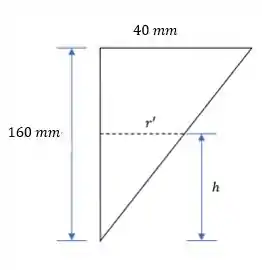
Temos:
E também, vamos utilizar o teorema de Pitágoras novamente para encontrarmos o valor da nova geratriz , que corresponde a posição do líquido no copo. Temos:
Substituindo na fórmula da área, temos:
É isso, galera, Bora resolver mais questões pra ficar craque.