Enunciado
Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 5.Problemas - Ex. 234
A figura mostra a seção transversal de um portão retangular de de altura e de comprimento (perpendicular ao papel) que bloqueia um canal de água doce. O portão tem uma massa de e é articulado em torno de um eixo horizontal através de . Calcule a força vertical exercida pela fundação na borda inferior do portão. Despreze a massa da estrutura à qual a porta está fixada.
Passo 1
Fala galera, tudo certo? Bora fazer mais um exercício? Prometo que vai ser bem rapidinho!
O enunciado nos pede para determinar a força vertical exercida pela fundação na borda inferior do portal de massa igual a , articulado em .
Então bora lá! Para resolver esse problema, vamos começar analisando o diagrama de corpo livre:
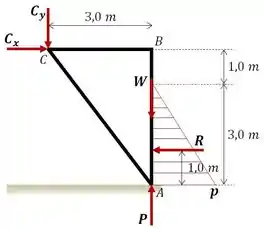
Onde o peso do portão é dado por:
Passo 2
Show de bola! Além do peso da estrutura, nós temos atuando à direita do portão a força exercida pela água, dada pela força distribuída cuja resultante chamamos de . Para determina-la, temos que a densidade da água é:
Logo, a pressão exercida pela água é:
Como essa pressão exercida pela água está atuando em uma área perpendicular ao plano da imagem de , a resultante no portão é:
E resultante está atuando a da base do portão, conforme mostrado no diagrama de corpo livre, pois se trata de uma força distribuída triangular.
Passo 3
Tranquilo né? Agora que já definimos a força resultante da pressão exercida pela água no portão e o peso dele, precisamos encontrar a força que a fundação exerce em sua borda inferior. Como ainda não temos as reações no pino articulado em e eles não são foco do nosso problema, vamos utilizar o equilíbrio de momentos em torno desse ponto para determinar a força :
É isso, galera. Até que foi tranquilo né?
Partiu pra próxima!
