Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Hibbeler - Estática- Ed: 14º - Capítulo 9.Problemas - Ex. 110

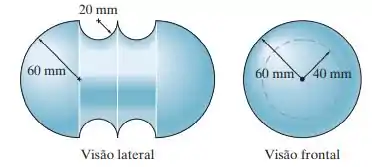
Determine o volume do material necessário para realizar a moldagem.

Passo 1

Fala aí, galerinha do Responde aí. Tudo bem? Bora pra mais uma questão de Estática.

Neste problema, temos que determinar o volume de material necessário para a moldagem desse sólido. Para isso, vamos utilizar o teorema de Pappus Guldin, ele é dado por:

V = θ r ¯ A

Onde θ é o ângulo de rotação que gera o corpo, neste caso, o meio-feio. Já A é área da região que vai gerar o sólido e r ¯ a distância do centroide da figura até o eixo de rotação.

Com isso, vamos determinar a área da região, temos:

Onde r 3 = r 2 - r 1 = 20   m m .

Como podemos observar, para esta região vamos ter a seguinte fórmula:

V = θ r ¯ A V = 2 π 2 π 4 r 2 2 4 r 2 3 π + 2 r 2 2 r 3 r 2 2 - 2 π 2 r 3 2 r 2 - 4 r 3 3 π V = 2 π 2 π 4 60 2 4 60 3 π + 2 60 2 ∙ 20 60 2 - 2 π 2 20 2 60 - 4 ∙ 20 3 π V = 140,28 × 10 4   m m 3

É isso, galera, Bora resolver mais questões pra ficar craque.

Resposta

V = 140,28 × 10 4   m m 3

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Calcule o volume V do sólido gerado pela revolução de 180° do triângulo retângulo em torno do eixo z.
O corpo mostrado em seção transversal é a metade de um anel circular obtido pela revolução de 180 graus da área sombreada em torno do eixo z . Determine a área superficial A do corpo.
Calcule o volume V do anel que tem a seção transversal mostrada.
Determine o volume V gerado pela revolução de 90 graus em torno do eixo z da área em forma de quarto de circulo.
A área mostrada é girada de 360 graus em torno do eixo y . Determine o volume do corpo resultante, que é uma esfera que tem uma parte significativa removida.