Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 7ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 7º - Capítulo 2.Problemas - Ex. 136
Um ônibus espacial está sujeito a impulsos de cinco dos motores de seu sistema de controle de reações. Quatro dos impulsos estão mostrados na figura; o quinto é um impulso de para cima, na traseira à direita, simétrico ao impulso de mostrado na traseira à esquerda. Calcule o momento destas forças em relação ao ponto e mostre que as forças têm o mesmo momento em relação a todos os pontos.
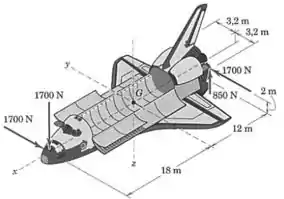
Passo 1
E aí gurizada tudo bem? Espero que sim!!!
Vamos calcular o momento total em relação ao ponto . Começamos com as duas forças de no plano , como elas têm a mesma direção e módulo, mas sentidos opostos, o momento é:
Onde F=força e D=distância
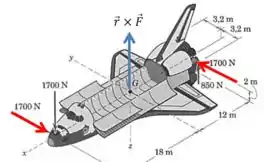
Galera se liga aí, o sinal negativo aparece porque a figura do enunciado define o sentido positivo como sendo “para baixo”. E a regra da mão direita para o produto vetorial indica que o momento aponta para cima.
Passo 2
Agora vamos olhar para a força de no bico do avião e para o par de forças de cada agindo na traseira.
Podemos tratar essas duas forças pensando na sua resultante agindo no ponto médio entre as duas, com um módulo de para cima:
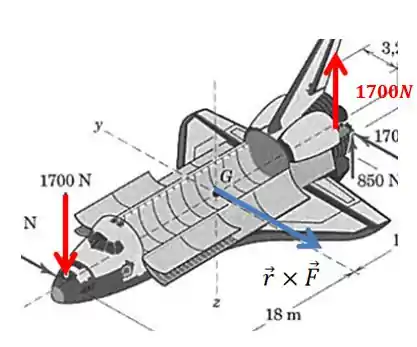
E dessa vez a regra da mão direita nos diz que o vetor momento aponta no sentido negativo do eixo (sentido anti horário) :D
Passo 3
Agora precisamos retornar às duas forças que consideramos no passo . Naquele caso consideramos o vetor entre as duas forças como estando paralelo ao eixo (de comprimento ), mas ele tem outra componente!
Perceba que existe um desnível de altura de entre os dois vetores, e essa outra componente do vetor deve apontar na direção desse desnível, de forma que a regra da mão direita vai dar o vetor momento na seguinte direção:
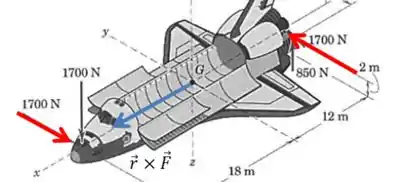
Galerinhaaa para exemplificar a regra da mão direita, vamos olhar para a força vermelha que age na traseira. Aponte seu indicador para cima na direção do desnível de , e depois seu dedo médio no sentido da força, seu polegar (quando esticado) vai estar apontando justamente na direção do vetor que desenhamos.)
E agora é só somar todos os momentos que calculamos:
Deixando na ordem correta, lembrando que x= i, y=j e K=y temos então....
Ahhhhhh galera se liga que os momentos estão em “KN” o que é a mesma coisa que acrescentarmos 3 casas ao valor que o acompanha, exemplo: -51 KN= -51000, assim faremso para os demais , olhemm !!
Ufaaa acabou!!
Mas antes temos que mostrar que independente do ponto, o momento em todos os pontos seria o mesmo...
Isso vai acontecer, por que temos aqui atuando vários binários de forças, e independente do ponto o momento gerado pelo binário é o mesmo...
Vamos ver isso, olhando o momento gerado pelo segundo par de forças...
Independente do ponto , a distância do binário vai ser a mesma e vale ... imagina um outro ponto qualquer, teríamos algo assim ó:
A distância entre as forças continua o mesmo ;)
Resposta
O momento total em relação ao ponto é .