Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 13.Problemas - Ex. 10

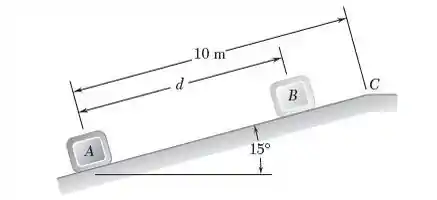
Um pacote é lançado para cima num aclive de 15 ° em A com velocidade de 8 m/s. Sabendo que o coeficiente de atrito cinético entre o pacote e a inclinação é 0,12 , determine (a) a máxima distância d que o pacote se moverá para cima na inclinação, (b) a velocidade do pacote quando este retornar a sua posição original.

Passo 1

Olá!! Tudo certo? Neste problema devemos encontrar (item a) a máxima distância d que o pacote percorrerá quando partir de A até B, subindo a inclinação. Em seguida, devemos encontrar (item b) a velocidade do pacote quanto este retorna do ponto B ao ponto A, descendo a inclinação.

(a) Subindo o plano de A até B.

Consideramos que:

v A = 8   m / s

T A = 1 2 ⋅ m ⋅ v A 2

T B = 0

U A → B = ( - W ⋅ s e n 15 ° - F ) d

F = μ ⋅ N

Como ∑ F = 0 :

N - W ⋅ cos ⁡ 15 ° = 0

N = W ⋅ cos ⁡ 15 °

E

F = μ ⋅ N = 0,12 ⋅ W ⋅ cos ⁡ 15 °

Logo, utilizando o princípio de trabalho e energia, temos:

T A + U A → B = T B

1 2 ⋅ W g ⋅ v A 2 + [ - W s e n 15 ° + 0,12 cos ⁡ 15 ° d ] = 0

1 2 ⋅ W g ⋅ 8 2 + [ - W s e n 15 ° + 0,12 cos ⁡ 15 ° d ] = 0

32 ⋅ W g + [ - W d 0,3747 ] = 0

d = 32 9,81 ⋅ 0,3747 = 8,7   m

(b) Agora iremos calcular a velocidade quando o pacote desce o plano, saindo de B em direção à A.

Consideramos que:

T B = 0

T A = 1 2 ⋅ m ⋅ v A 2

U B → A = ( W ⋅ s e n 15 ° - F ) d

Mais uma vez utilizando o princípio de trabalho e energia, temos:

T B + U B → A = T A

0 + W s e n 15 ° - 0,12 cos ⁡ 15 ° 8,7 = 1 2 ⋅ W g ⋅ v A 2

v A 2 = 2 9,81 ( 1,245 )

v A = 4,94     m / s

Resposta

(a) 8,7   m

(b) 4,94     m / s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

3/132) A esfera é liberada a partir da posição A com uma velocidade de 3m / s e oscila em uma plano vertical . Na posição maisi baixa , o cordão bate na barra fixa em B , e a esfera continua a oscilar
3/123) Aunidade motora A é utilizada para elevar o cilindro de 300k g a uma taxa constante de 2m / s . Se o medidor de potência B registra uma entrada de potência elétrica de 2,20k W , calcule a efici
3/134) O sistema é liberado a partir do repouso na posição mostrada . O cilindro de 15k g cai através do orifício no suporte , mas o disco de 15k g ( mostrado em corte) é removido do cilindro quando e
3/121) Um carro com uma massa de 1500k g parte do repouso na base de uma inclinação de 10 % e adquire uma velocidade de 50k m / h em uma distância de 100m com aceleração constante para cima na inclina
3/122) A resistência R à penetração x de um projétil de 0,25k g disparado com uma velocidade de 600m / s em um bloco de material fibroso é apresentada no gráfico . Represente essa resistência pela lin