Enunciado
Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 13.Problemas - Ex. 43
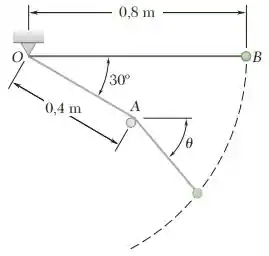
Uma pequena esfera de massa é liberada do repouso na posição mostrada na figura e oscila livremente em um plano vertical, primeiro em torno do ponto e em seguida em torno do pino , depois que a corda entra em contato com o pino. Determine a tração na corda (a) logo antes dela entrar em contato com o pino, (b) logo após dela entrar em contato com o pino.
Passo 1
Vamos lá! Como estamos em um capítulo que trabalha com trabalho e energia, vamos utilizar esta metodologia para resolver esta questão!
Mas, não é por isto que não devemos identificar as forças do nosso problema e construir um diagrama de corpo livre. Inclusive, este ponto é fundamental para entendermos a sacada do problema!
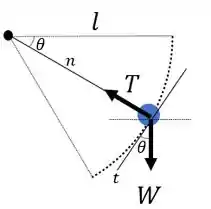
Por que a tração na corda vai mudar ao entrar em contato com o pino em A??? Vamos entender este ponto agora após fazermos o diagrama de corpo livre de uma esfera em trajetória circular! Sendo assim, temos:
Passo 2
Após fazermos o diagrama de corpo livre, vamos fazer o somatório das forças na direção normal. Desta forma, temos:
Esta relação é a mesma para o caso em que a corda não está em contato com o pino e está em contato com o pino.
Mas qual é a diferença? Bom, a massa é a mesma. A velocidade também (a gravidade nem precisamos comentar não é). O ângulo é 30°.
Até aqui é tudo o mesmo! E afinal, qual a diferença???
Bom, a diferença é o último parâmetro que não comentamos, o raio de curvatura . Antes de entrar em contato com o pino , o raio é . Após entrar em contato, o raio de curvatura é .
Passo 3
Agora que entendemos a diferença entre cada caso, podemos calcular a tração na corda!
Mas, antes disto, vamos calcular a velocidade da esfera logo antes de entrar em contato com o pino. Para isto, vamos ter de utilizar a metodologia de trabalho e energia.
Como a esfera parte do repouso e atinge uma velocidade , a energia cinética é:
Já para o trabalho, consideramos apenas a força peso, visto que a tração na corda é perpendicular a trajetória da esfera. Portanto,
Portanto, pelo princípio de trabalho e energia, temos:
Passo 4
Agora sim podemos calcular as trações na corda. Para a letra a), antes de entrar em contato com o pino , temos:
Já para a letra b), após entrar em contato com o pino , temos:
E assim finalizamos a questão!