Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 3.6 - Ex. 132
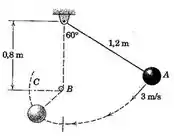
3/132) A esfera é liberada a partir da posição com uma velocidade de e oscila em uma plano vertical . Na posição maisi baixa , o cordão bate na barra fixa em , e a esfera continua a oscilar no arco tracejado . Calcule a velocidade da esfera quando esta passa a posição .
Passo 1
Então pessoal , para resolvermos esta questão devemos lembrar da equação de trabalho-energia que afirma que o trabalho total realizado por todas as forças é igual a variação na energia cinética da partícula :
Sendo assim ,
Isolando na equação , obtemos que :
Com isso , achamos que :
Resposta
Tranquilo pessoal? Então partiu resolver mais questões
Exercícios de Livros Relacionados
Se o coeficiente de atrito cinético entre a caixa de 100 kg e o plano é μ k = 0,25 , determine a velocidade da caixa no instante que a compressão da mola é x = 1,5 m. Inicialmente, a mola não está def
Bolas de gude tendo massa de 5 g caem do repouso em A através do tubo de vidro e se acumulam na vasilha em C . Determine a posição R da vasilha no fim do tubo e a velocidade na qual as bolas de gude c
Se a pista deve ser projetada de maneira que os passageiros do carro da montanha-russa não sintam uma força normal igual a zero ou mais do que 4 vezes o seu peso, determine as altura limitantes h A e
A roda de 80 kg tem um raio de giração em relação a seu centro de massa O, ko = 400 mm. Determine a velocidade angular após haver completado 20 revoluções, partindo do repouso.
A roda de 50 kg é submetida a uma forca d 50 N. Se a roda parte do repouso e rola sem deslizar, determine sua velocidade angular depois de haver completado 10 revoluções. O raio de giração da roda em