Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 3.6 - Ex. 122

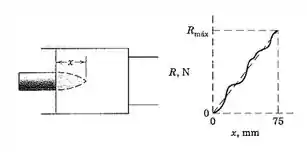
3/122) A resistência R à penetração x de um projétil de 0,25   k g disparado com uma velocidade de 600   m / s em um bloco de material fibroso é apresentada no gráfico . Represente essa resistência pela linha tacejada e calcule a velocidade v do projétil para o instante em que x = 25   m m se o projétil é levado a parar após uma penetração total de 75   m m .

Passo 1

Então galera , para resolvermos este exercício teremos que utilizar a equação de trabalho-energia , na qual :

U = ∆ T

Sendo assim , para x = 75   m m :

1 2 0,075 R m á x = 1 2 0,25 600 2

R m á x = 1,2   M N

Passo 2

Bom pessoal , para esta nova configuração em que x = 25   m m , podemos calcular a resistência pela relação :

R = x x m á x R m á x

R = 25 75 1,2 = 0,4   M N   o u   0,4 10 6 N

Agora teremos que usar novamente a equação de trabalho-energia para acharmos a velocidade pedida :

U = ∆ T

Substituindo os valores que já conhecemos e isolando v na equação , obtemos que :

1 2 0,025 0,4 10 6 = 1 2 0,25 600 2 - v 2

v 2 = 320 10 3 m s 2

v = 566   m / s

Resposta

R m á x = 1,2   M N

v = 566   m / s

Suave galera? Então bora resolver mais questões como essa!

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O disco uniforme de 6k g gira livremente em relação a um eixo horizontal através de O . Uma barra esbelta de 2k g é fixada ao disco conforme indicado. Se o sistema é levemente deslocado do repouso enq
A alavanca O A de 5,5k g com 250m m de raio de giração em relação a O está inicialmente em repouso na posição vertical ( θ = 90 ° ), onde a mola anexa de rigidez k = 525N / m está sem deformação. Calc
O disco B rola sem deslizar para baixo na inclinação A , que se desloca com velocidade v . Descreva o trabalho realizado pelas forças normal e de atrito que atuam sobre o disco para os casos (a) v = 0
O disco semicircular de massa m = 2k g está montado no aro leve de raio r = 150m m e é liberado a partir do repouso na posição (a). Determine a velocidade angular ω do aro e a força normal N sob o aro
O tambor de 375m m de raio e seu eixo possuem uma massa de 41k g e um raio de giração de 300m m em relação ao eixo de rotação. Um total de 18m de cabo de aço flexível com uma massa de 3,08k g por metr