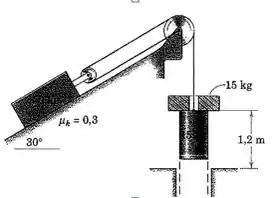
3/134) O sistema é liberado a partir do repouso na posição mostrada . O cilindro de cai através do orifício no suporte , mas o disco de ( mostrado em corte) é removido do cilindro quando este bate no suporte . Determine a distância que o bloco de sobe no plano inclinado . O coeficiente de atrito dinâmico entre o bloco e o plano inclinado é , e a massa da polia é desprezível .

Então galera , a primeirca coisa que devemos fazer é encontrar a força de atriti cinético através da relação :

Agora faremos uso da equação de trabalho-energia , na qual :

Sendo assim , para o primeiro intervalo :

Isolando na equação :

Logo ,