Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Hibbeler - Estática- Ed: 14º - Capítulo 10.Problemas - Ex. 89

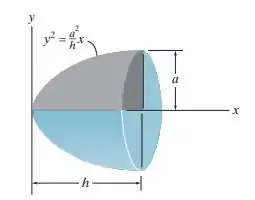
O paraboloide é formado girando-se a área sombreada em torno do eixo x . Determine o momento de inércia em relação ao eixo x e expresse o resultado em termos da massa total m  do paraboloide. O material tem densidade constante ρ .

Passo 1

Fala aí, galerinha do Responde aí. Tudo beleza? Vamos fazer mais uma questão de Estática.

Este problema nos pede para determinarmos o momento de inercia em relação ao eixo x da figura em termos da massa. Sabemos que ele é dado por:

I x = ∫ y 2   d A

Onde y é a distância perpendicular do eixo até o elemento d m . Primeiro, temos que determinar o elemento diferencial:

Em seguida, como o corpo é constituído por um material de densidade ρ , temos que:

d m = ρ   d V = π y 2   d x

Substituindo o elemento d V pelo volume do paraboloide, temos:

d m = ∫ π y 2   d x

Passo 2

Com isso, vamos calcular o momento de inercia do elemento, ele é dado por:

d I x = y 2 2 d m = 1 2 ρ π y 4   d x

Integrando a equação por todo o paraboloide, temos:

I x = ∫ 0 h 1 2 ρ π a 2 h x 2   d x   I x = 1 6 π ρ a 4

Opa, encontramos o momento de inercia, porém, o enunciado nos pede para encontramos o momento em termos da massa. Por isso, vamos determinar a massa:

m = ∫ ρ   d V = ∫ 0 h 1 2 ρ π a 2 h x   d x   m = 1 2 π ρ a 2

Por fim, basta substituirmos a massa no momento de inercia. Assim, o nosso resultado vai ser:

I x = 1 3 m a 2

É isso, galera, Bora resolver mais questões pra ficar craque.

Resposta

I x = 1 3 m a 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Calcule o momento de inércia de um aro (um anel fino) de raio R e massa M em relação a um eixo perpendicular ao plano do aro passando pela sua periferia.
9.20P Um cone homogêneo tem massa M , altura h e base de raio R . Calcule o momento de inércia em relação a um eixo perpendicular ao eixo do cone e passando pelo seu centro de massa. Sugestão: divida
O bloco homogêneo da figura abaixo, tem massa 0,172 Kg e lados a=3,5 cm, b=8,4 cm e c=1,4 cm. Calcule o momento de inercia do bloco em relação a um eixo que passa por um canto e é perpendicular às fac
Se o centro de massa do corpo não fosse colocado no eixo de rotação da mesa giratória, como o momento de inércia medido da pessoa se relaciona com o momento de inércia para rotação em torno do centro
Determine o momento de inercia em relação ao eixo x .