Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 5.Problemas - Ex. 53
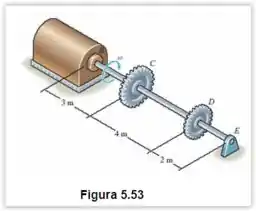
A turbina desenvolve de potência, que é transmitida às engrenagens de tal modo que recebe 70% e recebe 30%. Se a rotação do eixo de aço A-36 de de diâmetro for , determine a tensão de cisalhamento máxima absoluta no eixo e o ângulo de torção da extremidade do eixo em relação a . O mancal em permite que o eixo gire livremente em torno de seu eixo.
Passo 1
Olá, pessoal! Tudo bem com vocês?
O nosso problema pede que determinemos a tensão de cisalhamento máxima absoluta no eixo e o ângulo de torção da extremidade do eixo em relação a . Ele nos fornece como dados:
Aço A-36, portanto,
No enunciado, a rotação está em , então precisamos convertê-la para .
Ele nos diz que a engrenagem recebe 70% da potência da turbina e engrenagem recebe 30%, portanto, calculando:
Passo 2
Sabemos que a potência é dada por:
Então podemos calcular os torques fazendo:
Calculando o torque agindo na seção , temos:
Na engrenagem , temos:
E na engrenagem :
Passo 3
Para encontramos a tensão de cisalhamento máxima absoluta no eixo, usamos:
Em que é o raio e o momento polar de inércia, , é dado por:
Que substituindo em , fica:
Aplicando os valores, temos:
Passo 4
Para calcularmos o ângulo de torção, usamos a seguinte fórmula:
Que substituindo o , fica:
Observando o diagrama de corpo livre, vemos que o torque na seção é igual ao torque na engrenagem , ou seja:
O ângulo de torção da extremidade do eixo em relação a é encontrado fazendo-se a soma de e .
Passo 5
Substituindo os dados, temos:
Convertendo para graus: