Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 8.Problemas - Ex. 69
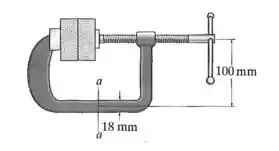
O parafuso da prensa exerce uma força de compressão de 2,5 kN nos blocos de madeira. Determine a tensão normal máxima desenvolvida ao longo da seção a-a. Nesse lugar, a seção transversal é retangular com dimensões 18 mm por 12 mm.
Passo 1
Fala, querido! Aqui a gente vai precisar achar os esforços normais e de momento nessa seção para achar as tensões normais, beleza?!
E para achar isso, precisamos perceber que esse esforço de compressão de dos bloquinhos de madeira é transmitido para a peça.
Para achar os esforços na nossa seção, é só cortar a peça nela, e descartar um dos lados. Vamos ser esperto, e ficar com o lado onde a gente já conhece a aplicação da força de .
Essa situação toda fica assim:
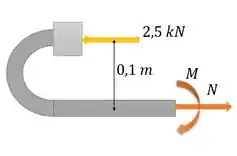
Faremos somatório de força na seção, obtemos que:
E fazendo o mesmo para o momento:
Tão aí os nossos esforços internos!
Passo 2
Agora para calcular a tensão normal máxima levamos em conta a força axial (normal à seção) e a torção pelo momento.
A tensão máxima causada pelo momento vai ocorrer no ponto mais distante da linha neutra, ou seja, em
Como a força normal vai causar tensão, precisamos considerar a região que tem essa distância da linha neutra e também causa tração, para encontrarmos a tensão máxima.
Assim, nossa tensão é:
Onde o momento de inércia da seção.