Enunciado
Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 2.Problemas - Ex. 95
Como parte de um teste de projeto, a roda dentada de acionamento do eixo de comando é fixada e, em seguida, as duas forças mostradas são aplicadas a uma correia enrolado em torno da roda dentada. Encontre a resultante desse sistema de duas forças e determine onde sua linha de ação intercepta os eixos x e y.
Passo 1
Fala galera! Tudo certo? Vamos dividir a resolução em algumas etapas, beleza? Esse problema parece um pouco mais complexo, mas vamos matar ele fácil fácil!
O enunciado nos pede duas coisas:
i) Calcular a resultante do sistema dado pelas forças e ;
ii) Determinar onde a linha de ação da resultante intercepta os eixos e .
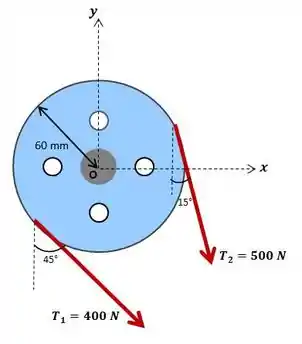
Pelo Princípio dos Momentos temos que:
Para encontrarmos a resultante neste caso, podemos analisar o somatório de forças em relação aos eixos e :
E o módulo da resultante:
Cujo ângulo com a horizontal é dado por:
Passo 2
Continuando, para encontrar o momento originado por esse somatório:
Obs: Note que e estão sendo aplicadas no perímetro da roda dentada, portanto suas distâncias até o ponto (braço de momento), é exatamente o raio da roda.
Passo 3
Por fim, precisamos definir uma resultante que dista do ponto e que, sozinha, equivale ao sistema força-binário original, ou seja:
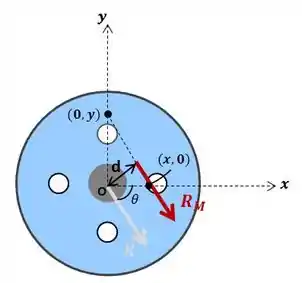
Essa força deve ser paralela a , ou seja, fazer um ângulo com a horizontal. Sendo assim, para determinar as coordenas e onde a linha de ação da resultante intercepta os eixos e , respectivamente, temos que:
Coordenada :
Coordenada :
Ufa! Essa já foi hein? Partiu pra próxima!
HYPERLINK "https://emojiterra.com/pt/rosto-piscando/" 