Enunciado
Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 3.Problemas - Ex. 2
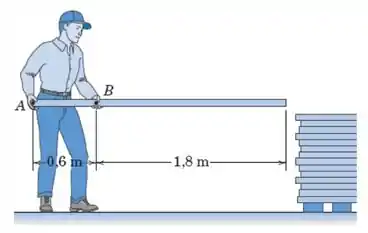
Um carpinteiro segura uma tábua uniforme com 6 kg, como mostrado. Determine as formas em A e B, se ele aplica forças verticais à tábua.
Passo 1
E aí meus queridxs, tudo bom com vocês?
Se liguem só, adotando que a tábua está em equilíbrio isso quer dizer que a resultante das forças em todas as direções deve ser igual a . Beleza, mas que forças são essas? Muito boa pergunta jovem gafanhoto
Pois bem, vamos desenhar essas forças na nossa bicicletinha
Lembrando que concentramos o peso da nossa barra no centro de massa que, para esse caso, fica no meio da nossa barra.
Passo 2
Pronto, com essa arte em mãos podemos partir pro ataque e resolver nosso problema que está, na verdade, praticamente resolvido. Como podemos notar não temos forças na direção , então, não precisaremos nos preocupar com essa direção. Analisando para a direção teremos
Adotando o sentido anti-horário como positivo vamos proceder de igual maneira para com o momento, que aqui calcularemos em relação ao ponto , obtendo o seguinte
Agora, para encontrarmos o valor de e concluirmos o exercício basta substituirmos em . Assim, obteremos
Pronto, está resolvido nosso exercício sem muito problema.