Enunciado
Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 2.Problemas - Ex. 127
A direção e o sentido das forças de 330 N podem variar, mas o ângulo entre elas é sempre 50°. Determine o valor de para que a resultante das forças atuantes em A seja na horizontal e para a esquerda.
Passo 1
Vamos começar o exercício desenhando o triângulo de forças para as duas forças de 330 N:
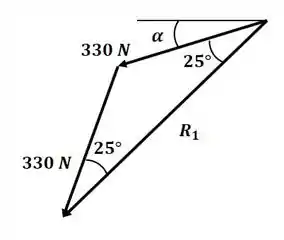
Agora podemos calcular a resultante por trigonometria:
Passo 2
Agora vamos desenhar o triângulo de forças para a força resultante do passo 1, a força de 1068 N e a resultante na horizontal e para a esquerda:
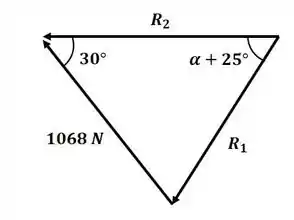
Agora, aplicando a lei dos senos para esse triângulo, temos:
Resposta
Exercícios de Livros Relacionados
A força F de 1800 N é aplicada à extremidade da viga em H. Expresse F como um vetor, usando os vetores unitários i e j.
A linha de ação da força F de 9,6k N passa pelos pontos A e B , como mostrado na figura. Determine os componentes escalares x e y de F .
Duas forças são aplicadas ao suporte de construção, como mostrado. Determine o ângulo θ que faz com que a resultante das duas forças seja vertical. Determine o módulo R da resultante.
A inclinação da força F de 4,8k N está especificada como mostrado na figura. Expresse F como um vetor, em termos dos vetores unitáriosi e j .
Por que, ao caminhar, o pé humano se comporta como uma alavanca inter-resistente? E por que, em uma mordida, o maxilar se comporta como uma alavanca interpotente?