Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 12.Problemas - Ex. 94

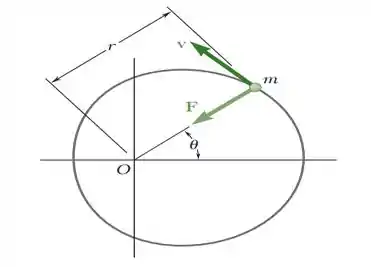
Uma partícula de massa m descreve uma cardioide r = r 0   (1 cos θ /2) sob uma força central F voltada para o centro de força O. Usando a Eq. (12.37), mostre que F é inversamente proporcional ao quadrado da distância r da partícula ao centro de força O.

Passo 1

E ai gurizada tudo belezinha??? O enunciado pede que a gente ), mostre que F é inversamente proporcional ao quadrado da distância r da partícula ao centro de força O.

Temos d 2 u d θ ² + u = F m h 2 u ²

Onde: u = 1 r e m h 2 = c o n s t a n t

F × u 2   d 2 u d   θ ² + u  

Agora: u = 1 r = 2 r 0 1 1 + c o s   θ  

Então: d u d θ = d d θ 2 r 0 1 1 + c o s   θ = 2 r 0 s i n   θ ( 1 + c o s   θ ) ²

E d 2 u d θ ² = 2 r 0 c o s   θ 1 + c o s   θ 2 - s i n θ   [ 2 1 + c o s θ ] ( - s i n θ ) ( 1 + c o s θ )

= 2 r 0 1 + c o s θ + s i n ² θ ( 1 + c o s θ ) ³ = 2 r 0 1 1 + c o s   θ 2 + 1 - c o s ² θ 1 + c o s   θ 3

= 2 r 0 2 - c o s θ ( 1 + c o s θ ) ² = 2 r 0 r 0 2 r ² 2 - ( 2 r r 0 - 1 ) = r 0 2 r ² 3 - 2 r r 0

Então: F × 1 r ² r 0 2 r ² 3 - 2 r r 0 + 1 r = 3 2 r 0 2 r 4

Resposta

a) F × 1 r 4

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Solucione o Problema 12.190 se a partícula tiver uma aceleração angular de θ ¨ = 5r a d / s 2 quando θ ˙ = 4r a d / s a θ = π / 2r a d .
A superfície parcial da came é uma espiral logarítmica r = 40 e 0,05 θm m , onde θ é dado em radianos. Se a came gira a uma velocidade angular constante de θ ˙ = 4r a d / s , determine as intensidades
A fenda do braço A B impulsiona o pino C pela fenda espiral descrita pela equação r = 1,5 θ m , onde θ é dado em radianos. Se p braço sai do repouso quando θ = 60 ° e é impulsionado a uma velocidade a
Determine a velocidade escalar do bloco A se a extremidade B da corda é puxada para baixo com uma velocidade escalar de 1,5m / s .
Determine a velocidade escalar do bloco A se a extremidade B da corda é puxada para baixo com uma velocidade escalar de 6m / s .