Enunciado
Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 12.Problemas - Ex. 90
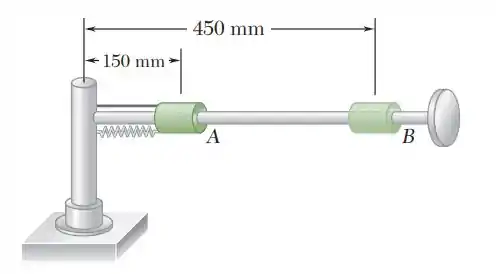
Um colar de 1,5 kg pode deslizar em uma haste horizontal que é livre para girar sobre um eixo vertical. O colar é inicialmente mantido preso ao eixo em A por uma corda. A mola de constante 35 N/m é fixada ao colar e ao eixo e não está deformada quando o colar está em A. No momento em que a haste gira a uma taxa 16 rad /s, a corda é cortada e o colar move-se ao longo da haste. Desprezando o atrito e a massa da haste, determine (a) as componentes radial e transversal da aceleração do colar em A, (b) a componente transversal da velocidade do colar em B.
Passo 1
E ai gurizada tudo belezinha???
Primeira nota:
(a)
Passo 2
(b)
Notar que :
Ou
Passo 3
(C) Depois que o cordão é cortado, a única força horizontal que atua no colar é devido à mola. Assim, o momento angular em torno do eixo é conservado.
Onde
Então:
Resposta
C )