Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 6.Problemas - Ex. 51

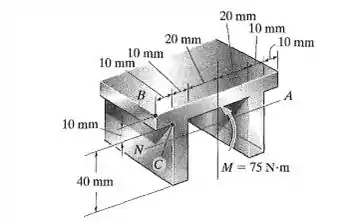
A peça de máquina feita de alumínio está sujeita a um momento M = 75 N.m. Determine a tensão de flexão criada nos pontos B e C da seção transversal. Trace um rascunho dos resultados sobre um elemento de volume localizado em cada um desses pontos.

Passo 1

Falaa galerinha do RespondeAí, tudo beleza?

Saca só, nesse exercício aqui o enunciado nos diz que uma peça de máquina feita de alumínio está sujeita a um momento M = 75   N .m . Sabendo disso ele nos pede para determinar a tensão de flexão criada nos pontos B e C da seção transversal.

Vamos, primeiro, calcular a coordenada y do centróide:

y c g = 2 × 20 10 × 40 + 40 + 5 × 80 × 10 2 10 × 40 + 80 × 10

y c g = 32,5   mm

Calculando o momento de inércia, teremos:

I = 2 0,01 × 0,04 3 12 + 0,01 × 0,04 0,0325 - 0,02 2 + 0,08 × 0,01 3 12 + 0,08 × 0,01 × 0,045 - 0,0325 2

I = 3,6333 10 - 7   m 4

Passo 2

Logo, podemos calcular as tensões:

σ b = 75 0,05 - 0,0325 3,6333 10 - 7 = 3,61 M P a

σ c = 75 0,04 - 0,0325 3,6333 10 - 7 = 1,55 M P a

Resposta

σ b = 3,61 M P a

σ c = 1,55 M P a

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determinar as equações das curvas dos diagramas de força cortante e de momento fletor para a viga com o carregamento mostrado e determinar também o máximo valor absoluto,
Determinar as equações das curvas dos diagramas de força cortante e de momento fletor para a viga com o carregamento mostrado. Determinar também o máximo valor absoluto fletor na viga.
Determinar as equações das curvas dos diagramas de força cortante e de momento fletor para a viga com o carregamento mostrado. Determinar também o máximo valor absoluto fletor na viga.
Uma viga A B é um sólido de revolução de diâmetro variável d . Para a porção A C da viga, expressar d , em termos de d 0 ,x e L , sabendo-se que a viga deve ser de igual resistência quando suporta o c
Um tubo de aço com diâmetro de 101,6 mm deve suportar o carregamento mostrado na figura. Sabendo que o estoque de tubos disponíveis tem espessuras que variam de 6 mm e 24 mm em incrementos de 3 mm, e