Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 5ª Edição - Russel C. Hibbeler- Ed: 5º - Capítulo 6.Problemas - Ex. 48
A peça de máquina feita de alumínio está sujeita a um momento . Determine as tensões de flexão máximas tanto de tração quanto de compressão na peça.
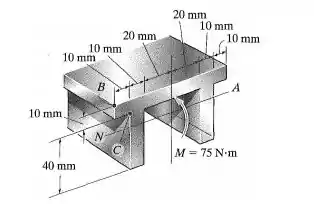
Passo 1
Fala aí pessoal, partiu mais um problema de resmat. Ele pediu as tensões máximas de compressão e tração nesse cara, e nos deu um momento. Então vamos usar a fórmulinha da tensão causada por momento para calcular essas bonitas. Bora!
Primeiramente, a gente vai começar observando as propriedades geométricas dessa seção.
Devemos calcular a coordenada do centroide da peça (pois ela possui eixo de simetria em ). Temos as duas peças retangulares verticais que são posionadas de forma simétrica, então a gente só multiplica os valores de uma por dois. E o retângulo de cima que está deitado.
O será dado por:
Agora, podemos determinar o momento de inérciaele será dado por:
Fazendo a conta, teremos:
Passo 2
Temos tudo agora para montar a fórmulinha da tensão:
é o momento dado, é o momento de inércia calculado. Quem é ?
Cara, ele é a distância do eixo horizontal que passa pelo centroide até o ponto onde nossa tensão é calculada. A tensão vai ser máxima nas extremidades da peça mais longes desse eixo.
Para descobrir que é de tração e quem é de compressão, olhamos a orientação do momento. Vemos que na parte de cima da peça, ele causa compressão e na parte de baixo ele causa tração.
Sendo assim, para compressão, nosso vale:
E para a tração: