Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 6.Problemas - Ex. 47

A peça de mármore, que podemos considerar como um material linear elástico frágil, tem peso específico de 24   k N / m ³ e espessura de 20   m m . Calcule a tensão de flexão máxima na peça se ela estiver apoiada ( a ) em seu lado e ( b ) em suas bordas. Se a tensão de ruptura for σ r u p = 1,5   M P a , explique as consequências de apoiar a peça em cada uma das posições.

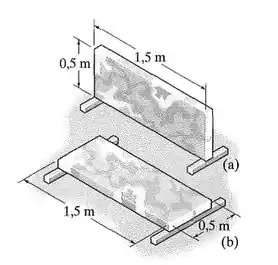
Passo 1

Fala ai galerinha do RespondeAí, tudo belejóia?

Para resolvermos essa questão, precisamos saber calcular a tensão de flexão máxima, que é dada pela multiplicação do momento máximo pela distância até a linha neutra, divididos pelo momento de inércia da peça. Por isso, vamos fazer o diagrama do corpo livre:

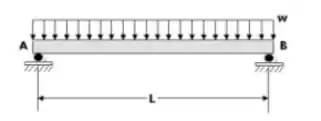
Passo 2

Iradoso, agora precisamos lembrar que o momento máximo para esse esquema é dado por:

M = w L 8

Portanto, precisamos calcular o a força peso para substituirmos na fórmula do momento:

w = y × V w = 24 × 10 3 0,5 × 1,5 × 0,02 w = 360   N

Substituindo, ficamos com:

M m á x = w L 8 M m á x = 360   N ( 1,5   m ) 8 M m á x = 67,5   N . m

Passo 3

Vamos agora calcular o momento de inércia I para cada caso. Para a , temos:

I a = b × h 3 12 I a = 0,02 × 0,5 3 12 I a = 2,08 × 10 - 4   m 4

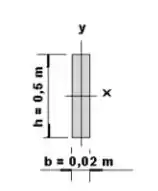
Para ( b ) :

I b = b × h 3 12 I b = 0,5 × 0,02 3 12 I b = 3,33 × 10 - 7   m 4

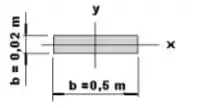
Passo 4

Por fim, basta substituirmos na fórmula de tensão de flexão máxima e comparamos com a tensão de ruptura para saber se a peça vai ou não romper.

Para ( a ) :

σ m á x = M m á x c I

σ m á x = 67,5 × 0,5 2 2,08 × 10 - 4   m 4   σ m á x = 0,081   M P a 0,081   M P a ≤ σ r u p

E para b :

σ m á x = M m á x c I

σ m á x = 67,5 × 0,02 2 3,33 × 10 - 7   m 4   σ m á x = 2,025   M P a σ r u p ≤ 2,025   M P a

Portanto, na posição ( a ) a peça resiste, mas na posição ( b ) a peça se rompe.

Resposta

σ m á x = 0,081   M P a

σ m á x = 2,025   M P a

Portanto, na posição ( a ) a peça resiste, mas na posição ( b ) a peça se rompe.

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

(a) Usando funções de singularidade, escreva as equações para a força cortante e o momento fletor para a viga e o carregamento mostrados. (b) Determine a tensão normal máxima provocada pelo momento fl
(a) Usando funções de singularidade, escreva as equações para a força cortante e o momento fletor para a viga e o carregamento mostrados. (b) Determine a tensão normal máxima provocada pelo momento fl
(a) Usando funções de singularidade, escreva as equações para a força cortante e o momento fletor para a viga e o carregamento mostrados. (b) Determine o valor máximo do momento fletor na viga.
(a) Usando funções de singularidade, determine a intensidade e a localização do momento fletor máximo para a viga e o carregamento mostrados. (b) Determine a tensão normal máxima provocada pelo moment
Uma viga está sendo projetada para ser vinculada e carregada conforme mostra a figura. (a) Usando funções de singularidade, encontre a intensidade e a localização do momento fletor máximo na viga. (b)