Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 6.Problemas - Ex. 71
O elemento tem seção transversal com as dimensões mostradas na figura. Determine o maior momento M que pode ser aplicado sem ultrapassar as tensões de tração e compressão admissíveis de (σt)adm = 150 MPa e (σc)adm = 100MPa, respectivamente.
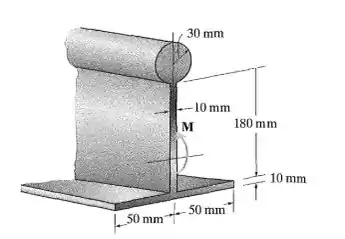
Passo 1
Primeiro, vamos determinar a coordenada do centróide:
Agora, podemos calcular o momento de inércia:
Passo 2
Com as tensões, podemos calcular os momentos para cada uma:
Devemos então escolher o menor valor para o momento, que será
Resposta
Exercícios de Livros Relacionados
A viga AB, consistindo em uma placa de alumínio de espessura uniforme b e comprimento L e, deve suportar a força mostrada. (a) Sabendo que a viga deve ser de resistência constante, expresse h em termo
Uma força transversal P é aplicada como mostrado na extremidade A do cone cônico AB. Chamando de do o diâmetro do cone em A, mostre que o máximo tensão normal máxima ocorre no ponto H, que está contid
Um projeto preliminar para o uso de uma viga de madeira prismática simplesmente apoiada indicou que seria necessária uma viga com uma seção transversal retangular de 50 mm de largura e 200 mm de altur
Considerando que o comprimento e a largura das placas de reforço utilizadas com a viga do Prob. 5,12 são, respectivamente, l = 4 me b = 285 mm, e lembrando que a espessura de cada placa é de 16 mm, de
Duas placas de reforço, cada uma com 7,5 mm de espessura, são soldadas a uma viga W460 x 74 conforme mostrado. Sabendo que l = 5 me b = 200 mm, determine a tensão normal máxima é de 150MPa para a viga