Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 6.Problemas - Ex. 45

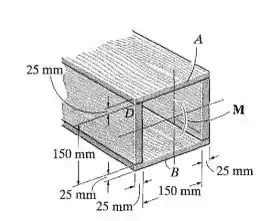
A viga está sujeita a um momento M. Determine a porcentagem desse momento à qual resistem as tensões que agem nas pranchas superior e inferior A e B da viga.

Passo 1

Primeiramente, vamos determinar o momento de inércia:

I = 0,2 × 0 , 2 3 12 - 0,15 × 0,15 3 12 = 9,1146 × 10 - 5

Vamos calcular as tensões em E e D:

σ e = M × 0,1 9,1146 × 10 - 5 = 1097,143 M

σ d = M × 0,075 9,1146 × 10 - 5 = 822,85 M

Passo 2

Podemos calcular a força resultante multiplicando a tensão pela área:

F r = 1097,143 M + 822,85 M 0,025 0,2 = 4,8 M

Logo, o momento gerado por essa força será:

M r = 0,17619 F r = 0,8457 M

Portanto, a porcentagem será:

100 % M r M =   100 % 0,8457 M M = 84,6 %

Resposta

84,6 %

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Dois perfis U de aço laminado devem ser soldados entre si ao longo das extremidades das mesas para suportar o carregamento mostrado na figura. Sabendo que a tensão normal admissível para o aço utiliza
(a) utilizando funções de singularidade, encontre a intensidade e posição do máximo momento fletor a viga e carregamento mostrados, (b) determine a tensão normal máxima em razão da flexão.
A viga AB, consistindo em uma placa de alumínio de espessura uniforme b e comprimento L, suporta a carga mostrada. (a) sabendo que a viga tem resistência constante, expressa h em termos de x , Leh 0 n
Uma viga em balanço AB consistindo em uma placa de altura constante h e largura b variável suporta a carga concentrada P no ponto A. (a) sabendo que a viga é de resistência constante, expresse b em te
Três placas de aço são soldadas juntas para formar a viga mostrada. Sabendo que a tensão normal admissível para o aço utilizado é de 22 ksi, determine a largura mínima b do flange que poderá ser usada