Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 3.Problemas - Ex. 22

Pede-se: (a) Para o eixo vazado mostrado e uma dada tensão admissível, determinar a relação T / w , sendo T o máximo torque admissível e w o peso por unidade de comprimento do eixo; (b) chamando de T w 0 o valor da relação calculada para um eixo maciço de mesmo raio c 2 , expressar a relação T / w para o eixo vazado, em termos de T w 0 e c 1 / c 2

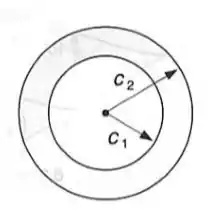
Passo 1

Para esse problema iremos calcular a tensão cisalhamento máxima utilizando a equação do torque:

τ m á x = T ⋅ c 2 J

Onde:

  • τ Representa a tensão de cisalhamento.
  • T A torção a qual a barra está submetida.
  • c A distância do centro ao ponto de aplicação.
  • J O momento de inércia polar.

Lembrando que o momento de inércia polar é calculado, para tubos vazados como:

J = π ⋅ c e x t 4 2 - π ⋅ c i n t 4 2

Passo 2

Para achar a relação T / w vamos calcular primeiro o torque:

τ m á x = T ⋅ c 2 J

T = τ m á x ⋅ J c 2

Com o momento de inércia polar igual a

J = π ⋅ c 2 4 2 - π ⋅ c 1 4 2

J = π ⋅ ( c 2 4 - c 1 4 ) 2

Assim

T = τ m á x ⋅ π ⋅ ( c 2 4 - c 1 4 ) 2 c 2

T = τ m á x ⋅ π ⋅ ( c 2 4 - c 1 4 ) 2 ⋅ c 2

Passo 3

Agora o termo w , peso por unidade de comprimento é igual a

w = P L

w = m g L

E a massa pode ser dada por

m = V o l ⋅ ρ

Logo

w = V o l ⋅ ρ g L

w = A ⋅ ρ ⋅ g

Como a área é igual a

A = π ⋅ ( c 2 2 - c 1 2 )  

w = π ⋅ ( c 2 2 - c 1 2 )   ⋅ ρ ⋅ g

Passo 4

Subsituindo em

T / w

T w = τ m á x ⋅ π ⋅ ( c 2 4 - c 1 4 ) 2 ⋅ c 2 ⋅ 1 π ⋅ ( c 2 2 - c 1 2 )   ⋅ ρ ⋅ g

Aplicando a igualdade

( c 2 4 - c 1 4 ) = ( c 2 2 + c 1 2 ) ⋅ ( c 2 2 - c 1 2 )

T w = τ m á x ⋅ π ⋅ ( c 2 2 + c 1 2 ) ⋅ ( c 2 2 - c 1 2 ) 2 ⋅ c 2 ⋅ 1 π ⋅ ( c 2 2 - c 1 2 )   ⋅ ρ ⋅ g

T w = τ m á x ⋅ ( c 2 2 + c 1 2 ) 2 ⋅ c 2 ⋅ 1 ρ ⋅ g

Passo 5

Agora vamos fazer o cálculo de T w 0 que é o caso de um eixo maciço:

Para achar a relação T w 0 vamos calcular primeiro o torque:

τ m á x = T ⋅ c 2 J

T = τ m á x ⋅ J c 2

Com o momento de inércia polar igual a

J = π ⋅ c 2 4 2

Assim

T = τ m á x ⋅ π ⋅ c 2 4 2 c 2

T = τ m á x ⋅ π ⋅ c 2 3 2

Passo 6

Agora o termo w , peso por unidade de comprimento é igual a

w = P L

w = m g L

E a massa pode ser dada por

m = V o l ⋅ ρ

Logo

w = V o l ⋅ ρ g L

w = A ⋅ ρ ⋅ g

Como a área é igual a

A = π ⋅ c 2 2  

w = π ⋅ c 2 2 ⋅ ρ ⋅ g

Passo 7

Calculando T w 0

T w 0 = τ m á x ⋅ π ⋅ c 2 3 2 ⋅ 1 π ⋅ c 2 2 ⋅ ρ ⋅ g

T w 0 = τ m á x c 2 2 ⋅ 1 ρ ⋅ g

Comparando com o eixo vazado

T w = τ m á x ⋅ ( c 2 2 + c 1 2 ) 2 ⋅ c 2 ⋅ 1 ρ ⋅ g

Temos

T w = T w 0 ⋅ c 2 2 + c 1 2 c 2 2

Resposta

a)

T w = τ m á x ⋅ ( c 2 2 + c 1 2 ) 2 ⋅ c 2 ⋅ 1 ρ ⋅ g

b)

T w = T w 0 ⋅ c 2 2 + c 1 2 c 2 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma amostra cilíndrica de 25m m de diâmetro está submetida a uma torque T . Determinar o valor do torque T , para que a amostra falhe e que tipo de falha (tração ou cisalhamento), se esta amostra for
Um torque de 1,75k N m é aplicado ao cilindro maciço mostrado. Determinar:A máxima tensão de cisalhamento;O percentual do torque absorvido pelo núcleo de diâmetro 25m m .
Determinar:A máxima tensão de cisalhamento provocada por um torque T de 4,5k N m em um eixo maciço de alumínio e 75 m m de diâmetro, como indicado:Idem ao item a, considerando que o eixo maciço deve s
Determinar:O torque T que causará uma tensão de cisalhamento máxima de 45M p a no cilindro vazado de aço, como indicado;A máxima tensão de cisalhamento causada pelo mesmo torque T, em um eixo cilíndri