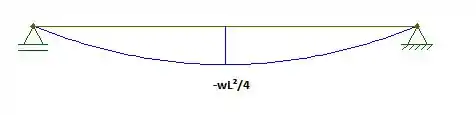
Pede-se: (a) Para a viga com o carregamento mostrado, determinar a distância , se o máximo valor absoluto do momento fletor na viga deve ser tão pequeno quanto possível; (b) Desenhar o diagrama de momento fletor correspondente.
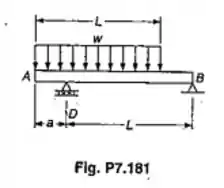
Passo 1
Fala aí galera do Responde aí, bora garantir aquele notão em resmat.
Para essa questão, vamos usar um pouco de cálculo. Quando queríamos achar o mínimo de uma função, o que fazíamos? Tínhamos que derivar ela e igualar a 0, depois descobrir se é um ponto de máximo ou mínimo. Lembrou?
Primeiro, vamos fazer um esboço do diagrama para entendermos onde fica o momento máximo.
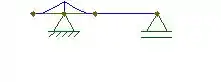
Vamos lá, o próximo passo é calcular o momento máximo em função das variáveis dadas. Sabemos que o momento de maior valor está no apoio D, e é dado por:
Derivando em relação a e igualando a 0
Portanto, o momento é mínimo quando
Passo 2
Agora, basta fazer o diagrama de momento fletor para a estrutura correspondente. Fazendo o diagrama:
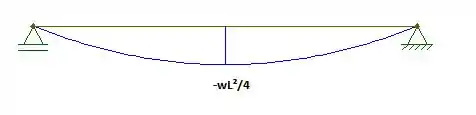
Resposta