Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 7.Problemas - Ex. 15

Desenhar os diagramas de força cortante e do momento fletor para a viga com o carregamento mostrado e determinar o máximo valor absoluto: a) força cortante b) momento fletor.

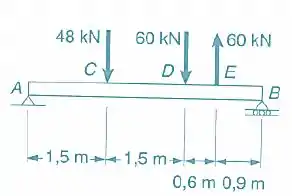
Passo 1

E ai gurizada tudo beleza? Espero que sim!!

Bom olha só, como no diagrama do exercício temos força aplicada na barra. Portanto vamos encontrar as reações em A e em B (VA e VB)... Considerando a setinha para baixo com valores negativos ..

Ahhhh se liga, da esquerda para a direita ;)

Partiu?

Σ M A = 0

Σ M A = - 48 × 1,5 - 60 × 3 + 60 × 3,6 + V B × 4,5 = 0

- 72 - 180 + 216 + 4,5 × V B = 0

V B = 8 K N

Agora gurizadaaaa o somatório das forças na vertical (Y)

Σ F y = V A - 48 - 60 + 60 + 8 = 0

V A = 40   K N

Passo 2

Agora vamos determinar a força cortante? Vem comigo!!!

Para realizarmos esse diagrama pensem comigo, eu falei para vocês antes que a seta para baixo é negativo certo?

Então no 1º quadrante fica igual= a VA pois temos um apoio antes da carga=40 KN

2º quadrante: como temos a reação VA positiva, o cálculo da força será assim: 40-48 = - 8 K N  

3º quadrante: usamos o resultado anterior menos a força aplicada: - 8 - 60 = - 68 K N

4º quadrante: - 68 + 60 = - 8  

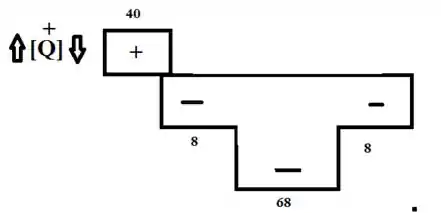
Passo 3

Agora vamos calcular comigo o momento fletor, 3 cargas, 3 momentos fletores, basta multiplicarmos a força pela distância expressa no diagrama

M A = 0

M B = 8 × 0,8 = 6,4   K N × m

M C = 40 × 1,5 = 60 N × m

M C = 40 × 3 - 48 × 1,5 = 48   K N × m

M D = 8 × 0,8 = 6,4   K N × m

Agora sim podemos desenhar o diagrama, CUIDADO com os sinais ;)

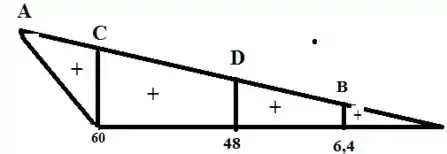
Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Para o sistema eixo-engrenagem e carregamento do Prob. 7.156, determinar o menor diâmetro permissível para o eixo maciço C D .
Assumindo que o eixo do Prob. 7.158 é vazado e que o diâmetro interno é metade do diâmetro externo, determinar o menor diâmetro externo permissível para o eixo.
Resolver o Prob. 161, assumindo que toda a potência de 25h p é absorvida pela engrenagem G .
Resolver o Prob. 162, assumindo que 25k W é absorvido em cada engrenagem.
Determinar a carga uniformemente distribuída admissível w , para a viga mostrada, sabendo-se que σ a d m = + 70M P a na tração, σ a d m = - 130M P a , na compressão, e que τ a d m = 60M P a .