Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Hibbeler - Estática- Ed: 14º - Capítulo 10.Problemas - Ex. 105

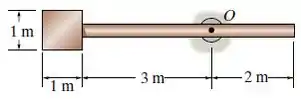
O pêndulo consiste em uma placa com peso de 60 kg e uma haste fina com peso de 20 kg. Determine o raio de giração do pêndulo em relação a um eixo perpendicular à página e que passa pelo ponto O .

Passo 1

E aí Pessoal, tudo bem? Vamos dar início a mais uma questão juntos!

Precisamos calcular o raio de giração do pêndulo em relação a um eixo perpendicular à página e que passa pelo ponto O (que não passa pelo centro de massa da haste e da placa!!!).

Para calcularmos o raio de giração, basta relembrarmos da seguinte relação:

k = I m

Sendo I o momento de inércia do pêndulo em relação ao eixo O e m a massa do pêndulo 80   k g .

Então, precisamos determinar o momento de inércia primeiramente para depois calcular o raio de giração.

Então, vamos as contas!

Passo 2

Vamos calcular o momento de inércia da haste e da placa em relação a um eixo perpendicular que passa pelo seu centro de massa. Começando pela haste, temos:

I h a s t e = m L 2 12 = 20 ⋅ 5 2 12 = 41,667   k g ⋅ m 2

Já para a placa será:

I p l a c a = m a 2 + b 2 12 = 60 1 2 + 1 2 12 = 5   k g ⋅ m 2

Só que nós não podemos somar os dois momentos diretamente, pois eles são calculados em relação ao centro de massa deles. Por causa disso, precisamos utilizar o teorema dos eixos paralelos, que nos diz que:

I = I G + m d 2

Sendo I G o momento de inércia que passa pelo centro de massa da peça, I o momento de inércia que queremos e d a distância entre os dois eixos.

Para o caso da questão, o centro de massa da haste dista d h a s t e = 0,5   m . Já a placa dista d p l a c a = 3,5   m .

Portanto, o momento de inércia do sistema será:

I O = I h a s t e + m h a s t e d h a s t e 2 + I p l a c a + m p l a c a d p l a c a 2

I O = 41,667 + 20 ⋅ 0,5 2 + 5 + 60 ⋅ 3,5 2

I O = 786,67   k g ⋅ m 2

E assim determinamos o momento de inércia do sistema.

Passo 3

Para finalizarmos a questão, basta calcularmos o raio de giração. Portanto,

k = 786,67 80

k = 3,14   m

E assim finalizamos a questão!

Resposta

k = 3,14   m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine o raio de giração k x do sólido formado girando-se a área sombreada em relação ao eixo x . A densidade do material é r .
O pêndulo consiste em um disco A de massa 8k g , um disco B de 2k g e uma haste fina de 4k g . Determine o raio de giração do pêndulo em relação a um eixo perpendicular à página e que passa pelo ponto
O cone circular reto é formado girando-se a área sombreada em torno do eixo x . Determine o momento de inércia I x e expresse o resultado em termos da massa total m do cone. O material tem densidade c
Determine o momento de inércia I x e expresse o resultado em termos da massa total m do cone. A esfera possui densidade constante ρ .
O pêndulo consiste em uma haste fina de 3k g e uma placa fina de 5k g . Determine a localização y do centro de massa G do pêndulo; depois, determine o momento de inércia de massa do pêndulo em relação