Enunciado
Mecânica e Resistência dos Materiais - Hibbeler - Estática- Ed: 14º - Capítulo 11.Problemas - Ex. 43
Cada elemento tem uma massa por comprimento . Determine os ângulos e nos quais eles estão suspensos em equilíbrio. O contato em é liso, e ambos são conectados por um pino em .
Passo 1
Fala galera, tudo certo? Bora fazer mais um exercício? Prometo que vai ser bem rapidinho!
O enunciado nos pede para determinar os ângulos e necessários para que o corpo esteja em equilíbrio. Considerando que cada elemento possui massa por unidade de comprimento .
Então bora lá! Para resolver esse problema, vamos começar analisando o diagrama de corpo livre:
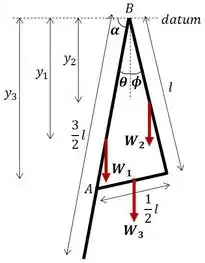
Onde as distâncias , e são:
E os pesos , e das hastes:
Passo 2
Show de bola! Vamos começar então formulando a equação da energia potencial desse sistema. Como temos atuando apenas os pesos das hastes:
Passo 3
Grandinha a equação né?
Mas calma, para facilitar nossos cálculos vamos encontrar a relação entre os ângulos e . Começando pelo cálculo da reta :
Logo:
Passo 4
Agora que nós temos a equação da energia potencial do sistema, para analisar o equilíbrio do corpo, podemos fazer a derivada de em relação a e o resultado deve ser zero. Ou seja:
Passo 5
E, finalmente, a partir desse ângulo , podemos determinar e necessários para que a estrutura esteja em equilíbrio:
Do Passo 3 temos que , logo:
É isso, galera. Essa foi grande hein?
Partiu pra próxima!
