Enunciado
Física - Hibbeler - Estática- Ed: 14º - Capítulo 10.Problemas - Ex. 96
O pêndulo consiste em um disco de massa , um disco de e uma haste fina de . Determine o raio de giração do pêndulo em relação a um eixo perpendicular à página e que passa pelo ponto .
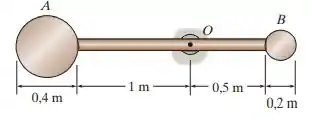
Passo 1
Fala aí, galerinha do Responde aí. Tudo beleza? Vamos fazer mais uma questão de Estática.
Para determinarmos o momento de inércia de massa sobre um eixo através de , temos que determinar o momento de inércia de cada segmento de haste e segmento de disco em torno de um eixo passa por seu centro de massa pode ser determinado usando as seguintes relações:
Assim, o momento de inercia em torno de vai ser:
Então, sabendo que a massa total vai ser:
Por fim, sabemos que o raio de giração é dado por:
É isso, galera, Bora resolver mais questões pra ficar craque.
Resposta
Exercícios de Livros Relacionados
O bloco homogêneo da figura abaixo, tem massa 0,172 Kg e lados a=3,5 cm, b=8,4 cm e c=1,4 cm. Calcule o momento de inercia do bloco em relação a um eixo que passa por um canto e é perpendicular às fac
Para a placa retangular fina indicada na parte (d) da tabela 9.2, ache o momento de inércia em relação a um eixo situado sobre o plano da placa passando pelo seu centro e paralelo ao eixo indicado na
Use o teorema dos eixos paralelos para mostrar que os momentos de inércia das partes (a) e (b) da Tabela 9.2 são coerentes.
Uma placa metálica fina de massa M tem forma retangular com lados a e b. Use o teorema dos eixos paralelos para determinar seu momento de inércia em relação a um eixo perpendicular ao plana da placa p
Uma corda leve e flexível é enrolada diversas vezes em torno da periferia de uma casca cilíndrica com raio de 0.25 m e massa igual a 40.0 N, que gira sem atrito em torno de um eixo horizontal fixo. O