Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 3.10 - Ex. 240
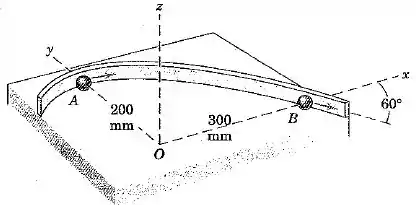
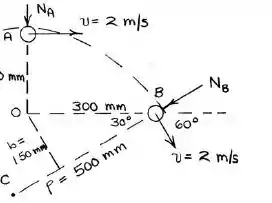
Uma pequena partícula de recebe uma velocidade de sobre o plano horizontal e é guiada pela barra curva fixa. O atrito é desprezível. Quando a partícula cruza o eixo em , sua velocidade é na direção , e quando ela cruza o eixo em , sua velocidade faz um ângulo de com o eixo . O raio de curvatura da trajetória em é . Determine a taxa de variação no tempo da quantidade de movimento angular da partícula em torno do eixo através de em ambos e .
Passo 1
Bom galera, nesse exercício queremos encontrar a taxa de variação no tempo da quantidade de movimento angular da partícula. Sabemos que
Passo 2
Em , temos que
Portanto,
Passo 3
Em , temos que
Resposta
Exercícios de Livros Relacionados
A esfera de 2k g está presa em uma barra leve e rígida, que gira no plano horizontal centrada em O . Se o sistema está sujeito a um momento de binário M = 0,9 t 2 N ⋅ m , onde t está em segundos, dete
A partícula A de 2k g tem a velocidade mostrada. Determine sua quantidade de movimento angular H P em relação ao ponto P .
Duas esferas idênticas de 10k g estão fixadas em uma barra leve e rígida, a qual gira no plano horizontal centrada em O . Se aas esferas estão sujeitas a forças tangenciais P = 10N , e a barra está su
O bloco de 5k g está girando em relação à trajetória circujlar centrada em O , sobre o plano horizontal liso, quando é submetido à força F = 10 t N , onde t está em segundos. Se o bloco parte do repou
A pá à frente do trator coleta neve a uma taxa de 200k g / s . Determine a força de tração resultante T , que deve ser desenvolvida em todas as rodas enquanto ele move-se para frente sobre o terreno p