Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 3.10 - Ex. 247
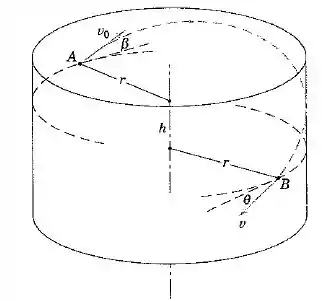
Uma partícula é liberada na parede interna lisa de um reservatório cilíndrico em com uma velocidade que faz um ângulo com a tangente horizontal. Quando a partícula atinge um ponto uma distância abaixo de , determine a expressão para o ângulo feito pela sua velocidade com a tangente horizontal em
Passo 1
Bom galera, nesse exercício queremos determinar uma expressão para o ângulo feito pela sua velocidade com a tangente horizontal em . Sabemos que o momento angular é conservado e, dessa forma, temos
Passo 2
Podemos escrever então
Dessa forma, temos
Passo 3
Pela conservação da energia, temos que
Substituindo, temos
Dessa forma, temos que
Resposta
Exercícios de Livros Relacionados
A barra A B de 2 kg está pendurada na posição vertical. Um bloco de 1 k g , deslizando sobre uma superfície horizontal lisa com uma velocidade de 3,6m / s , acerta a barra na sua extremidade B. Determ
A bola sólida de massa m é solta com uma velocidade v 1 sobre a aresta do degrau áspero. Se ela repica horizontalmente no degrau com uma velocidade v 2 , determine o ângulo no qual o contato ocorre. S
A bobina de 50 kg é submetida a uma força horizontal P = 150 N. Se a bobina rola sem deslizar, determine sua velocidade angular 3 s após ela partir do repouso. O raio de giração da bobina em relação a
A roda de 300 kg tem um raio de giração em relação a seu centro de massa O de k O = 400m m . Se a roda é submetida a um momento de binário M = 300N . m , determine sua velocidade angular 6 s após ela
As engrenagens A e B de massa 10 kg e 50 kg têm raios de giração em relação a seus centros de massa respectivos k A = 80m m e k B = 150m m . Se a engrenagem A é submetida ao momento de binário M = 10N