Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 17.Problemas - Ex. 121

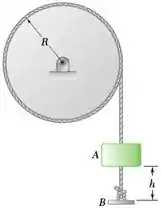
Uma pequena placa B é presa a uma corda que é enrolada em volta de um disco uniforme de 4 kg e raio R = 200 mm. Um cursor A de 1,5 kg é liberado do repouso e cai de uma distância h = 300 mm antes de atingir a placa B. Considerando que o impacto é perfeitamente plástico e desprezando o peso da placa, determine imediatamente após o impacto (a) a velocidade do cursor, (b) a velocidade angular do disco.

Passo 1

O colar A cai uma distância h. Do princípio de conservação de energia.

v 1 = 2 g h

Análise de impacto. Cinemática. Impacto plástico.

e = 0

O colar A e a placa B movem-se juntos. O cabo é inextensível.

v - 2 = R ω               o u                 ω 2 = v - 2 R

Seja m = massa do colar A e M = massa do disco

Momento de inércia do disco:

I - = 1 2 M R 2

+ Momentos sobre C:

m v 1 R = I - ω 2 + m v 2 R

m v 1 R = 1 2 M R 2 v 2 R + m v 2 R

m v 1 = 1 2 M v 2 + m v 2

v 2 = 2 m 2 m + M v 1

Passo 2

Dados:

m = 3   lb/g

M = 8   lb/g

h = 15   in. = 1.25   ft

R = 9   in. = 0.75   ft

v 1 = 2 32.2 1.25 = 8.972   ft/s

Passo 3

  1. Velocidade de A.

    2. v 2 = 2 3 2 3 + 8 v 1 = 3 7 v 1

    v 2 = 3 7 8.972 = 3.8452   ft/s

    Passo 2

  2. Velocidade angular.

ω 2 = 3.8452 0.75 = 5.13   rad/s 

Resposta

a )   v 2 = 3.85   ft/s↓

b )   ω 2 = 5.13   rad/s 

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A partícula A de 2k g tem a velocidade mostrada. Determine sua quantidade de movimento angular H O em relação ao ponto O .
A esfera de 2k g está presa em uma barra leve e rígida, que gira no plano horizontal centrada em O . Se o sistema está sujeito a um momento de binário M = 0,9 t 2 N ⋅ m , onde t está em segundos, dete
A partícula A de 2k g tem a velocidade mostrada. Determine sua quantidade de movimento angular H P em relação ao ponto P .
Duas esferas idênticas de 10k g estão fixadas em uma barra leve e rígida, a qual gira no plano horizontal centrada em O . Se aas esferas estão sujeitas a forças tangenciais P = 10N , e a barra está su
O bloco de 5k g está girando em relação à trajetória circujlar centrada em O , sobre o plano horizontal liso, quando é submetido à força F = 10 t N , onde t está em segundos. Se o bloco parte do repou