Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 2.4 - Ex. 76

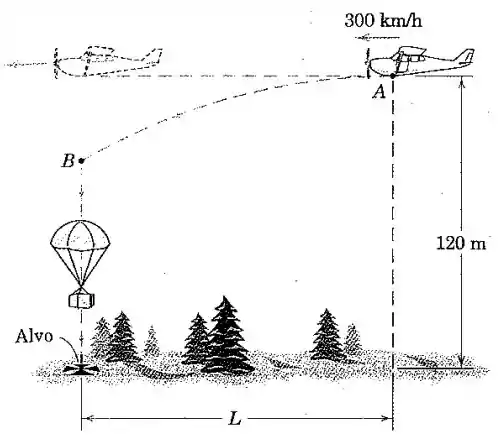
Um pequeno avião voando horizontalmente com uma velocidade de 300   k m / h em uma altitude de 120   m acima de um vale remoto deixa cair um pacote de emergência médica em A . O pacote tem um paraquedas que se abre em B e permite que o pacote desça verticalmente a uma taxa constante de 1,8   m / s . Se a queda é planejada de modo que o pacote atinja o solo em 37 segundos após a liberação em A , determine o adiantamento horizontal L de modo que o pacote atinja o alvo. Despreze a resistência atmosférica de A para B .

Passo 1

Galera, em todo esse processo, teremos dois momentos, com dois movimentos distintos. Analisaremos primeiro o movimento de A até B .

Teremos uma velocidade horizontal constante v x = 300   k m / h = 83,33   m / s , e portanto,

L = v x t B = 83,33 t B

onde t B é o tempo gasto para o pacote chegar até B .

Verticalmente, teremos:

y B = y A - 1 2 g t B 2 = 120 - 4,9 t B 2

Passo 2

Num segundo momento, a partir do ponto B   y 0 = y B , o pacote desce até o solo ( y = 0   m ) com velocidade constante ( v y = - 1,8   m / s ) durante um tempo t = 37 - t B :

y = y 0 + v y t

0 = y B - 1,8 37 - t B

Porém, da equação obtida no passo anterior, podemos pegar y B :

0 = 120 - 4,9 t B 2 - 66,6 + 1,8 t B

4,9 t B 2 - 1,8 t B - 53,4 = 0

A única raiz positiva dessa equação será t B = 3,5   s , e assim já podemos achar L :

L = 83,33 t B = 292   m

Resposta

L = 292   m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O carro tem uma velocidade escalar de 16.5 m/s. Determine a velocidade angular θ ˙ da linha radial O A nesse instante.
A cavilha P é inpulsionada pelo anel do garfo O A ao longo da trajetória curva descrita por r = e θ . Quando θ = π / 4 rad, o anel tem uma velocidade angular e a aceleração angular de θ ˙ = 2 rad/s e
A plataforma está girando em torno do eixo vertical de modo que em qualquer instante a sua posição angular é θ = ( 4 t 3 / 2 ) , onde t é dado em segundos. Uma bola rola para fora ao longo do sulco ra
Na parte baixa do loop em um plano vertical, um aeroplano tem velocidade de 150 m/s e está acelerando a uma taxa de 25 m/s2. O raio de curvatura do loop é 2.000 m. O aeroplano está sendo controlado pe
A partir de medições de uma fotografia, verificou-se que o fluxo de água mostrado na figura deixa o bocal em A e tem raio de curvatura de 25 m. Determine (a) a velocidade inicial vA do fluxo, (b) o ra