Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 2.4 - Ex. 70
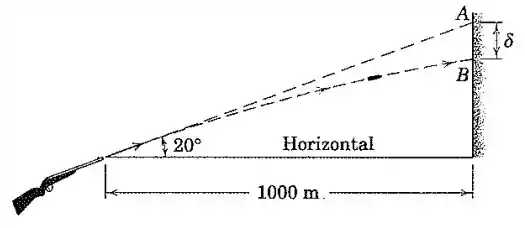
Se o cano da espingarda mostrada aponta para o ponto , calcule a distância abaixo de até o ponto onde a bala incide. A velocidade de saída no disparo da bala é de .
Passo 1
Galera, como o cano da espingarda faz um ângulo de com o eixo , podemos considerar que o vetor velocidade inicial da bala também faz esse mesmo ângulo, e portanto:
Mas, segundo o enunciado, , então:
Isso significa que as velocidades iniciais horizontal e vertical são:
Passo 2
Como não há arrasto aerodinâmico, podemos considerar a velocidade horizontal constante em todo o trajeto, e portanto:
Ou seja, a bala demora para alcançar o ponto .
Passo 3
Como a aceleração vertical é constante, temos que a altura durante o movimento é dada por:
Substituindo , obtemos a altura :
No entanto, olhando para o triângulo retângulo de base e um ângulo de , podemos achar a altura do ponto :
Portanto,