Enunciado
Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 7.Problemas - Ex. 39
O pequeno cilindro de massa me raio r está confinado a rolar na superfície circular do raio R. Pelos métodos deste artigo, prove que o cilindro é instável no caso (a) e estável no caso (b).
Passo 1
O exercício pede que a gente prove que o cilindro é instável no caso (a) e estável no caso (b).
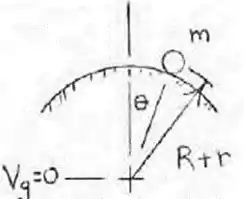
Passo 2
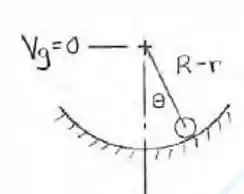
Resposta
(b)
Exercícios de Livros Relacionados
No projeto da garra para o atuador de ação remota, uma força de fixação C é desenvolvida como resultado da tensão P na haste de controle. Expresse C em termos de P para a configuração mostrada, onde a
Uma plataforma de carga elétrica projetada para a parte traseira de um caminhão é mostrada na figura. A posição da plataforma é controlada pelo cilindro hidráulico, que aplica força em C. Os links são
Resolva o problema 17.25, assumindo que o cilindro é substituído por um tubo de parede fina de raio r e massa m.17.25 - Uma corda é enrolada em torno de um cilindro de raio r e massa m, conforme mostr
Cada um dos elos uniformes idênticos tem um comprimento le uma massa me está sujeito a um par M, um no sentido horário e outro no sentido anti-horário, aplicado como mostrado. Determine o ângulo que c
Determine a força N exercida na tora por cada mandíbula das pinças para lareira mostradas.