Enunciado
Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 5.Problemas - Ex. 240
Como parte de um estudo de projeto preliminar, os efeitos das cargas de vento em um edifício de são investigados. Para a distribuição parabólica da pressão do vento mostrada na figura, calcule as reações de força e momento na base do edifício devido à carga do vento. A profundidade da construção (perpendicular ao papel) é de .
Passo 1
Fala galera, tudo certo? Bora fazer mais um exercício? Prometo que vai ser bem rapidinho!
O enunciado nos pede para determinar as reações de força e momento na base engastada do edifício de , considerando que sua profundidade perpendicular ao papel é de .
Então bora lá! Para resolver esse problema, vamos começar analisando o diagrama de corpo livre:
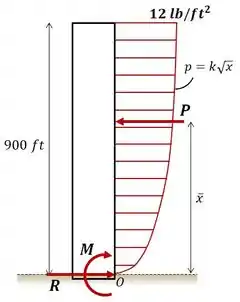
Lembrando que a profundidade do edifício para dentro da imagem é de .
A força distribuída ao longo do edifício pode ser substituída por uma resultante que calcularemos a seguir. Mas antes disso, já podemos notar de cara que, pela condição de equilíbrio do corpo, a resultante na base da fundação deve ser igual a essa força equivalente à carga distribuída:
E o momento resultante na base deve ser equivalente ao momento produzido pela força resultante nesse ponto, também pela condição de equilíbrio de momentos:
Passo 2
Show de bola! Conforme foi dito, a força distribuída ao longo do edifício é dada pela equação:
Onde a constante pode ser obtida pela pressão de na altura de :
Com isso, ficou fácil determinar a força resultante. Como o edifício possui uma profundidade de e altura de , temos que:
Passo 3
Além disso, precisamos ainda da posição do centroide onde está sendo aplicada:
Passo 4
Tranquilinho né? Agora podemos finalmente determinar a resultante do momento gerado por essa força :
É isso, galera. Até que foi de boa né?
Partiu pra próxima!
