Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 6.5 - Ex. 113
Os pequenos roletes nas extremidades da barra esbelta uniforme de estão limitados a se deslocar nas ranhuras que se situam em um plano vertical. No instante em que , a velocidade angular da barra é de no sentido horário. Determine a aceleração angular da barra, as reações em e , e as acelerações dos pontos e sob a ação da força de . Despreze o atrito e a massa dos pequenos roletes.
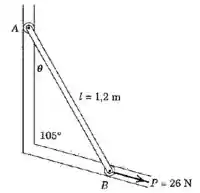
Passo 1
Vamos começar com um diagrama que represente as forças que agem sobre a barra:
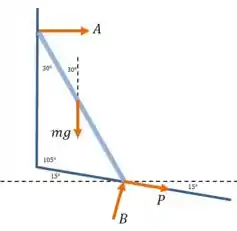
E então podemos aplicar a segunda lei de Newton nas direções vertical e horizontal:
E na horizontal:
E por fim, o momento resultante em relação ao centro de massa é:
Simplificando essa equação:
E então ficamos com um sistema de três equações:
Passo 2
Precisamos encontrar expressões para as componentes da aceleração do centro de massa.
Vamos começar olhando para a aceleração da roda em :
A aceleração da roda aponta na direção do eixo vertical então:
E a aceleração do centro de massa é:
E a acelerção relativa entre os dois terá uma componente tangencial e outra centrípeta:
E o vetor é a posição do ponto em relação ao centro de massa. Podemos escrever esse vetor olhando para o desenho:
Vamos usar isso para calcular os dois termos da aceleração relativa. Começando pela componete tangencial:
E agora a centrípeta:
Agora vamos substituir tudo na equação principal.
E podemos transformar essa equação vetorial em um sistema de duas equações, uma para cada componente:
Passo 3
Agora vamos fazer praticamente a mesma coisa, mas para a aceleração em . Muitas coisas serão iguais, ou muito parecidas:
A aceleração da roda tem componentes nos dois eixos, então:
E a aceleração do centro de massa é:
E a acelerção relativa entre os dois terá uma componente tangencial e outra centrípeta:
E o vetor é a posição do ponto em relação ao centro de massa. Podemos escrever esse vetor olhando para o desenho:
Vamos usar isso para calcular os dois termos da aceleração relativa. Começando pela componete tangencial:
E agora a centrípeta:
Agora vamos substituir tudo na equação principal.
E podemos transformar essa equação vetorial em um sistema de duas equações, uma para cada componente:
Passo 4
Podemos juntar tudo isso em um único sistema de sete equações:
E sete variáveis desconhecidas: (, , , , , , ). Vamos substituir os valores numéricos que conhecemos:
Resolver um sistema de sete equações manualmente pode ser quase impossível, então vamos simplesmente escrever o sistema em forma de matriz e depois usar um computador para resolver o problema:
E resolvendo esse sistema com algum programa, encontramos os seguintes valores:
E os demais valores não foram pedidos no enunciado.
Resposta
As forças são e . As acelerações são , e .