Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 6.5 - Ex. 108
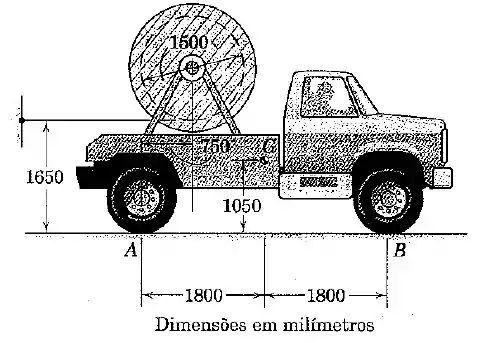
O caminhão transporta uma bobina com de diâmetro de um cabo com massa de por metro de comprimento. Existem voltas na bobina cheia. A bobina vazia possui uma massa de , com raio de giração de . O caminhão isolado possui uma massa de , com centro de massa em . Se o caminhão parte do repouso com uma aceleração inicial de , determine (a) a tração no cabo onde ele se prende à parede e (b) a reação normal sobre cada par de rodas. Despreze a inércia de rotação das rodas do caminhão.
Passo 1
(a) Para encontrar a tração no cabo, vamos considerar uma equação de momentos em relação ao centro da bobina:
Como a força peso age justamtne nesse centro , a única força que produz momento em torno desse ponto é a tração :
E para encontrar o momento de inércia total precisamos somar o da bobina vazia e da corda:
E a acelerção angular pode ser calculada usando a seguinte fórmula:
Já que a aceleração com que o cabo é puxado é igual à aceleração do caminhão que foi dada no enunciado:
E então:
Passo 2
(b) Agora queremos encontrar as reações normais e sobre cada par de rodas. Precisamos de um diagrama das forças que agem sobre o caminhão.
Além das duas forças e agindo nas rodas, temos o peso agindo no centro de massa e as forças de contato da bobina, na direção vertical () e horizontal :
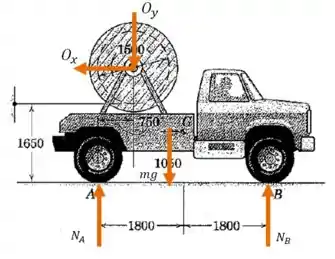
Para encontrar as componente e , nós podemos aplicar a segunda lei de Newton sobre a bobina:
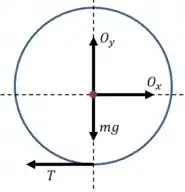
Começamos com a direção horizontal:
E as forças que agem nessa direção são e , então:
E na direção vertical:
Passo 3
Beleza, agora que conhecemos mais variáveis, vamos voltar a pensar no caminhão ao invés da bobina:
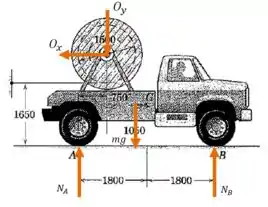
Como o caminhão se move com aceleração , a força resultante que age sobre o seu centro de massa é:
E essa força está a uma distância perpendicular de do ponto (ou ), então se escrevermos uma equação de momentos em relação a esse ponto:
E os momentos das outras forças em relação ao ponto podem ser calculados a partir do desenho:
Então:
E agora podemos usar a segunda lei de Newton na direção vertical para encontrar :
Resposta
(a) .
(b) e .