Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 5.6 - Ex. 154

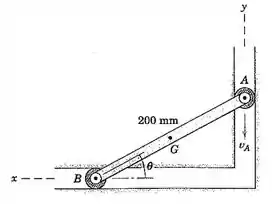
Se a extremidade A da barra restrita possui uma velocidade constante para eixo v A de 2 m/s quando a barra passa pela posição para qual θ = 30 ° , determine a aceleração do centro de massa G no meio da barra. Compare a solução pela álgebra vetorial pela geometria vetorial.

Passo 1

Galera, primeiro vamos organizar todos os dados do enunciado e fazer um esboço do que realmente importa no mecanismo.

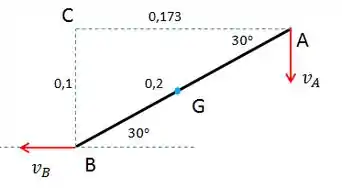
Primeiro, vamos resolver por álgebra vetorial.

Através do Centro instantâneo de Velocidade Nula (C), podemos calcular a velocidade angular da barra AB e a velocidade do ponto B:

ω = v A r A / C = - 2 0,173 = - 11,547 k ^   r a d / s

v B = ω × r B / C = - 11,547 k ^ × - 0,1 j ^ = - 1,155 i ^   m / s

Bom, agora vamos analisar o mecanismo. Esta etapa vai ser muito importante!! Vamos em tópicos:

-Sabemos que B está limitado ao curso do trilho, logo sua aceleração está obrigatoriamente na horizontal.

-Já o ponto A se move ao longo da vertical com velocidade constante, logo não há aceleração.

-Portanto o sistema não possui nenhuma aceleração na componente vertical. Isto limita a aceleração no ponto G na componente horizontal!

Beleza? Por isso é importante desenhar o diagrama e identificar o tipo de apoio em cada ponto!!

Agora, usamos a equação da aceleração relativa entre A e G:

a G = a A + a G / A n + a G / A t

Onde:

a G / A n = ω × ω × r G / A = - - 11,547 2 - 0,173 2 i ^ - 0,1 2 j ^ = 11,533 i ^ + 6,66 j ^ m / s 2

a G / A t = α A G × r G / A = α A G 0,1 2 i ^ - 0,173 2 j ^ m / s 2

a A = 0   m / s 2

Agora, vamos substituir os valores encontrados na equação da aceleração relativa:

a G i ^ =   0 + 11,533 i ^ + 6,66 j ^ + α A G 0,1 2 i ^ - 0,173 2 j ^

Decompondo nas direções, temos o sistema:

a G i ^ =   11,533 i ^ + α A G 0,1 2 i ^

0 =   6,66 j ^ + α A G - 0,173 2 j ^

Resolvendo o sistema, temos:

α A G = 7 7 k ^   r a d / s 2

a G = 15,3 5 i ^   m / s 2

Passo 2

Neste passo, vamos resolver por geometria vetorial. Para isso, vamos montar o diagrama de vetores aceleração.

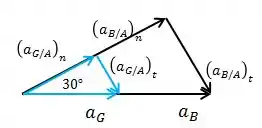
Vamos aos cálculos das acelerações:

a B / A n = r ω 2 = 0,2 11,547 2 = 26,67   m / s 2

a B / A t = r α = 0,2 α

Como o ponto G está no centro:

a B / A n = 1 2 a G / A n = 13,33   m / s 2

a B / A t = 1 2 a G / A t = 0,1 α

Pelo triangulo retângulo:

a G = a G / A n c o s 30 = 15,39   m / s 2

Resposta

a G = 15,39   i ^   m / s 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um recipiente para resíduos é descarregado pelo mecanismo ativado hidraulicamente. Se a haste do pistão parte do repouso na posição indicada e possui uma aceleração de 0,5 m/s² no sentido mostrado, ca
Determine a aceleração do ponto B no equador da Terra, reapresentado aqui a partir do Prob. 5/64. Utilize os dados Fornecidos naquele problema e assuma que a trajetória orbital da Terra é circular, co
O centro O do disco possui a velocidade e a aceleração indicadas na figura. Se o disco rola sem deslizar sobre a superfície horizontal, determine a velocidade de A e a aceleração de B para o instante
Um carro possui uma aceleração para frente a = 4 m / s 2 sem deslizar seus pneus de 600 mm de diâmetro. Determine a velocidade v do carro quando um ponto P sobre o pneu na posição indicada terá a comp
A viga de aço de 9m está sendo levantada a partir de sua posição horizontal pelos dois cabos presos em A e B. Se as acelerações angulares iniciais dos tambores de elevação são α 1 = 0,5r a d / s 2 e α