Enunciado
Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 5.Problemas - Ex. 125
Para o perfil cantoneira e o carregamento mostrado no Prob. Resolvido 5.8, verificar que , ao longo da perna vertical da cantoneira.
Passo 1
Vamos lá!
Temos que determinar o fluxo de cisalhamento em função de , do Problema resolvido 5.8.
A seguinte situação se apresenta para nós.
O fluxo de cisalhamento representa a força por unidade de comprimento ao longo do eixo longitudinal de uma viga. Esse valor de cisalhamento foi obtido pela fórmula já calculada do exercício:
Como estamos lidando com um exercício resolvido, vamos aproveitar de alguns desenhos.
Mas fiz um aqui para ficar mais rápido saca só!
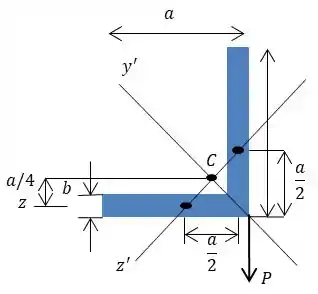
Passo 2
Como estamos lidando com apenas o eixo , a única variável que pode estar variando é nosso .
Teremos nosso variando de zero até seu valor máximo, logo, aplicando a integral a fórmula já calculada de cisalhamento da aba horizontal, temos:
Multiplicando o cisalhamento pela espessura da viga integrando pela sua variação de comprimento temos:
Integrando temos:
Aplicando os limites de integração temos:
Resposta
O cálculo comprovando que é a resposta.