Enunciado
Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 5.Problemas - Ex. 3
Resolva o Prob. 5.2, considerando que o espaçamento entra os pregos é aumentado para s = 100 mm
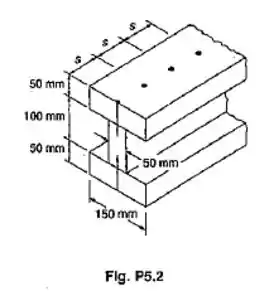
Passo 1
Do enunciado temos que
Nosso momento de inércia será dado por
Onde 1 representa a tábua superior, 2 a do meio e 3 a inferior.
Observe que é zero uma vez que o logo a distância entre eles é nula.
Vamos ter para a área da tábua 1 é
Adistancia entre a linha neutra total e o centro da tábua 1 é
Passo 2
Temos ainda para Q
Então o é dado por
Observe que nós queremos o valor de V. Temos ainda a relação:
Juntando isso temos:
Resposta
Exercícios de Livros Relacionados
A viga-mestra de alma dupla é composta por duas folhas de compensado presas a elementos de madeira na parte superior e na parte inferior. A tensão de flexão admissível para a madeira é σ a d m = 56M P
A viga é composta por três tiras de poliestireno coladas como mostra a figura. Se a cola tiver uma resistência ao cisalhamento de 80k P a , determine a carga máxima P que pode ser aplicada sem que a c
A viga é fabricada com dois perfis em U equivalentes e duas chapas. Cada chapa tem altura de 150 mm e espessura de 12 mm. Se um cisalhamento V = 250k N for aplicado à seção transversal, determine o es
A viga é feita com quatro tábuas pregadas como mostra a figura. Se cada um dos pregos puder suportar uma força de cisalhamento de 500N , determine os espaçamentos s ’ e s exigidos entre eles se a viga
Se a viga for submetida a um cisalhamento de V = 15 kN, determine a tensão de cisalhamento na alma em A e B. Indique as componentes da tensão de cisalhamento sobre um elemento de volume localizado nes